��Ŀ����
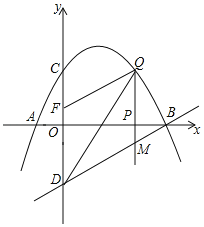
����Ŀ����ͼ����֪������y����![]() +bx+c��ͼ����A(��1��0)�͵�C(0��2)����D���C����x��Գƣ���P��x���ϵ�һ�����㣬���P������Ϊ(m��0)������P��x��Ĵ���l���������ڵ�Q����ֱ��BD�ڵ�M.
+bx+c��ͼ����A(��1��0)�͵�C(0��2)����D���C����x��Գƣ���P��x���ϵ�һ�����㣬���P������Ϊ(m��0)������P��x��Ĵ���l���������ڵ�Q����ֱ��BD�ڵ�M.
(1)�������������ʾ�Ķ��κ����ı���ʽ.
(2)��֪��F(0��![]() )������P��x�����������˶�ʱ������mΪ��ֵʱ���ı���DMQF��ƽ���ı��Σ�
)������P��x�����������˶�ʱ������mΪ��ֵʱ���ı���DMQF��ƽ���ı��Σ�
(3)��P���߶�AB�˶������У��Ƿ���ڵ�Q��ʹ���Ե�B��Q��MΪ��������������BOD���ƣ������ڣ������Q�����ꣻ�������ڣ���˵������.
���𰸡�(1)![]() ��(2) m��3��m��1+
��(2) m��3��m��1+![]() �� (3)���ڣ���Q������Ϊ(3��2)��(��1��0)
�� (3)���ڣ���Q������Ϊ(3��2)��(��1��0)
��������
(1)���ô���ϵ����ȷ����������ʽ��
(2)�����ô���ϵ�������ֱ��BD����ʽΪy��![]() x��2����Q(m����
x��2����Q(m����![]() m2+
m2+![]() m+2)��M(m��
m+2)��M(m��![]() m��2)����QM��DF���ı���DMQF��ƽ���ı���֪QM��DF��������������ٵ���P���߶�AB��ʱ�ڵ�P��AB���ӳ�����ʱ���ֱ��г�����m�ķ��̣���֮�ɵã�
m��2)����QM��DF���ı���DMQF��ƽ���ı���֪QM��DF��������������ٵ���P���߶�AB��ʱ�ڵ�P��AB���ӳ�����ʱ���ֱ��г�����m�ķ��̣���֮�ɵã�
(3)��֪��ODB����QMB���ʷ֢١�DOB����MBQ��90�������á�DOB�ס�MBQ��![]() ��
��![]() ����֤��MBQ�ס�BPQ��
����֤��MBQ�ס�BPQ��![]() ����
����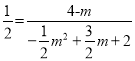 ����֮���ɵô�ʱm��ֵ���ڡ�BQM��90������ʱ��Q���A�غϣ���BOD�ס�BQM�����õ�Q����.
����֮���ɵô�ʱm��ֵ���ڡ�BQM��90������ʱ��Q���A�غϣ���BOD�ס�BQM�����õ�Q����.
(1)����A(��1��0)�͵�C(0��2)����y����![]() x2+bx+c�У���
x2+bx+c����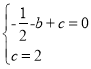 .
.
���![]() .
.
��������߽���ʽΪ��![]() ��
��
(2) ������֪��D����Ϊ(0����2)��
�ߵ�B����������x��������Ľ��㣬��![]() ��
��
���x=4��x=-1����ȥ����
��B������4��0����
��ֱ��BD����ʽΪy��kx+b��
��B(4��0)��D(0����2)���룬�ã�![]() ��
��
��ã�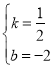 ��
��
��ֱ��BD����ʽΪy��![]() x��2��
x��2��
���������������
�ٵ���P���߶�AB��ʱ��
��QM��x�ᣬP(m
��Q(m����![]() m2+
m2+![]() m+2)��M(m��
m+2)��M(m��![]() m��2)��
m��2)��
��QM����![]() m2+
m2+![]() m+2��(
m+2��(![]() m��2)����
m��2)����![]() m2+m+4��
m2+m+4��
��F(0��![]() )��D(0����2)��
)��D(0����2)��
��DF��![]() ��
��
��QM��DF��
�൱��![]() m2+m+4��
m2+m+4��![]() ʱ���ı���DMQF��ƽ���ı��Σ�
ʱ���ı���DMQF��ƽ���ı��Σ�
��ã�m����1��m��3��
��m��0��
��m=3��
����m��3ʱ���ı���DMQF��ƽ���ı��Σ�
�ڵ�P��AB���ӳ�����ʱ��
��QM��x�ᣬP(m��0)(m��0)��
��Q(m����![]() m2+
m2+![]() m+2)��M(m��
m+2)��M(m��![]() m��2)��
m��2)��
��QM��![]() m��2��(��
m��2��(��![]() m2+
m2+![]() m+2)��
m+2)��![]() m2��m��4��
m2��m��4��
��F(0��![]() )��D(0����2)��
)��D(0����2)��
��DF��![]() ��
��
��QM��DF��
�൱![]() m2��m��4��
m2��m��4��![]() ʱ���ı���DMQF��ƽ���ı��Σ�
ʱ���ı���DMQF��ƽ���ı��Σ�
���m��![]() ��
��
��m��0��
��m��1+![]() ��
��
����m��1+![]() ʱ���ı���DMQF��ƽ���ı��Σ�
ʱ���ı���DMQF��ƽ���ı��Σ�
������������m��3��m��1+![]() ʱ���ı���DMQF��ƽ���ı��Σ�
ʱ���ı���DMQF��ƽ���ı��Σ�
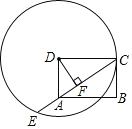
(3)��ͼ��ʾ��
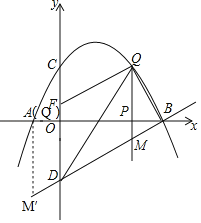
��QM��DF��
���ODB����QMB��
���������������
�ٵ���DOB����MBQ��90��ʱ����DOB�ס�MBQ��
��![]() ��
��
�ߡ�MBQ��90����
���MBP+��PBQ��90����
�ߡ�MPB����BPQ��90����
���MBP+��BMP��90����
���BMP����PBQ��
���MBQ�ס�BPQ��
��![]() ����
���� ��
��
��ã�m1��3��m2��4��
��m��4ʱ����P��Q��M�����B�غϣ����ܹ��������Σ���ȥ��
��m��3����Q������Ϊ(3��2)��
�ڵ���BQM��90��ʱ����ʱ��Q���A�غϣ���BOD�ס�BQM����
��ʱm����1����Q������Ϊ(��1��0)��
���ϣ���Q������Ϊ(3��2)��(��1��0)ʱ���Ե�B��Q��MΪ��������������BOD����.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�