��Ŀ����
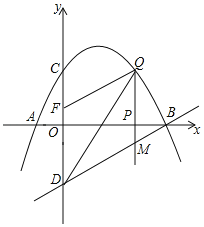
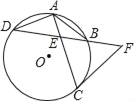
����Ŀ����ͼ1��![]() �У�
��![]() ��������
��������![]() ��ͼ1�ڷţ�ʹ���εİ뾶
��ͼ1�ڷţ�ʹ���εİ뾶![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �غϣ�
�غϣ�![]() ��
��
����������
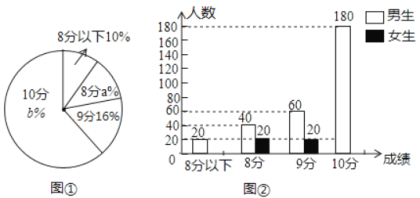
��ͼ2����![]() ������������
������������![]() �Ƶ�
�Ƶ�![]() ��ʱ����תһ�ܣ������߶�
��ʱ����תһ�ܣ������߶�![]() ��
��![]() ������ת��Ϊ
������ת��Ϊ![]() ��
��
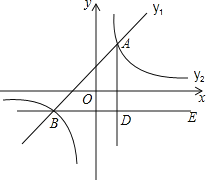
���֣�ֱ��д��![]() ��
��![]() ��������ϵ��
��������ϵ��
̽������![]()
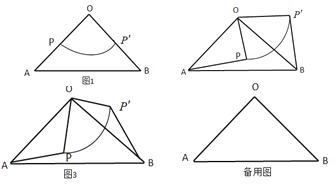
��1������![]() �Ƶ���
�Ƶ���![]() ����࣬��
����࣬��![]() ʱ����ת��
ʱ����ת��![]() ______�㣻
______�㣻
��2������![]() �Ƶ���
�Ƶ���![]() ���Ҳ࣬��
���Ҳ࣬��![]() ��
��![]() ����ʱ����
����ʱ����![]() ��
��
��3������![]() �ǻ�
�ǻ�![]() ������һ�㣬������
������һ�㣬������![]() �Ƶ�
�Ƶ�![]() ��ʱ��ת�����У���
��ʱ��ת�����У���![]() ��������ʱ��ֱ��д��
��������ʱ��ֱ��д��![]() �Ķ�����
�Ķ�����
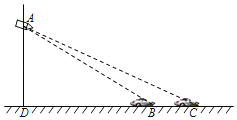
���죺��ͼ3����![]() ����
����![]() ��
��![]() ��
��![]() ���㹲��ʱ��ֱ��д���߶�
���㹲��ʱ��ֱ��д���߶�![]() �ij���
�ij���
���𰸡�����![]() ��̽������1��310����2��
��̽������1��310����2��![]() ����3��
����3��![]() ��
��![]() �����죺
�����죺![]() ��
��![]() ��
��
��������
���֣�����OA=OB��OP=O![]() ���ɵõ�
���ɵõ�![]() ��
��
̽������1���������⻭��ͼ�Σ���OP��AB�õ���AOP=��A=50�������������ת��![]()
![]() ��
��
��2����![]() ��
��![]() ���еõ�
���еõ�![]() ��ֱ�������Σ����ݹ��ɶ������AP���ɵõ�B
��ֱ�������Σ����ݹ��ɶ������AP���ɵõ�B![]() ��
��
��3������![]() �����=OQ���Թ���A��OQ�ĸ��ߵĻ���һ�룬�ʵ�����ǡ����OAʱ��
�����=OQ���Թ���A��OQ�ĸ��ߵĻ���һ�룬�ʵ�����ǡ����OAʱ��![]() ���������ɴ˵õ�
���������ɴ˵õ�![]() �Ķ�����
�Ķ�����
���죺�������⻭��ͼ�Σ����õ��������ε����ߺ�һ�����ʼ����Ǻ������OH�����ù��ɶ������AH�����ɵõ���.
���֣���OA=OB��OP=O![]() ��
��
��OA-OP=OB-O![]() ��
��
��![]() ��
��
̽����
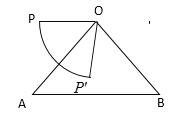
��1����ͼ��
��![]() ��OA=OB��
��OA=OB��
���A=��B=50����
��OP��AB��
���AOP=��A=50����
����ת��![]()
![]() ��
��
�ʴ�Ϊ��310��
��2���⣺��![]() ��
��![]() ����
����
��![]() ��
��![]() ��ֱ�������Σ�
��ֱ�������Σ�
��![]() ��
��
��![]() ��
��
��3���ߵ�Q��![]() �ϣ�
�ϣ�
��OQ=OP��
![]() �����=OQ���Թ���A��OQ�ĸ��ߵĻ���һ�룬�ʵ�����ǡ����OAʱ��
�����=OQ���Թ���A��OQ�ĸ��ߵĻ���һ�룬�ʵ�����ǡ����OAʱ��![]() ��������
��������
��![]() =90��-80��=10����
=90��-80��=10����![]() =180��-10��=170����
=180��-10��=170����
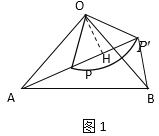
���죺����O��OH��P![]() ��H����ͼ1��
��H����ͼ1��
�ߡ�PO![]() =90����OP=O
=90����OP=O![]() =6��
=6��
��OH=PH=![]() ��
��
��OA=10��
��AH=![]() ,
,
��B![]() =AP=
=AP=![]() ��
��
����O��OH��P![]() ��H����ͼ2��
��H����ͼ2��
�ߡ�PO![]() =90����OP=O
=90����OP=O![]() =6��
=6��
��OH=PH=![]() ��
��
��OA=10��
��AH=![]() ,
,
��B![]() =AP=
=AP=![]() ��
��
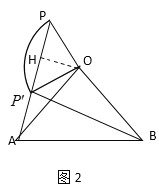
���߶�![]() �ij�Ϊ
�ij�Ϊ![]() ��
��![]() .
.

 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д�