题目内容
探究题.
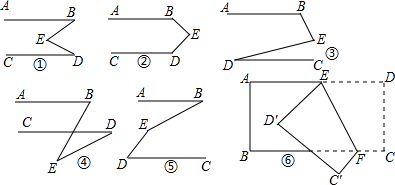
问题一:已知:AB∥CD,直接写出①②③④⑤图中∠B、∠E、∠D关系;
问题二:如图⑥,把长方形纸片ABCD沿EF折叠后,点D、C分别落在D′、C′位置,若∠EFB=60°,则
∠AED′= .(直接填空)
问题一:已知:AB∥CD,直接写出①②③④⑤图中∠B、∠E、∠D关系;
问题二:如图⑥,把长方形纸片ABCD沿EF折叠后,点D、C分别落在D′、C′位置,若∠EFB=60°,则
∠AED′=

考点:平行线的性质,翻折变换(折叠问题)
专题:
分析:(1)首先过点E作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,内错角相等,即可求得答案;
(2)首先过点E作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,同旁内角互补,即可求得答案;
(3)首先过点E作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,同旁内角互补,两直线平行,内错角相等,即可求得答案;
(4)由AB∥CD,根据两直线平行,同位角相等,即可求得∠1=∠B,又由三角形外角的性质,即可求得答案.
(5)首先过点E作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,同旁内角互补,两直线平行,内错角相等,即可求得答案;
(6)由AB∥CD,根据两直线平行,内错角相等,两直线平行,同旁内角互补即可求得答案.
(2)首先过点E作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,同旁内角互补,即可求得答案;
(3)首先过点E作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,同旁内角互补,两直线平行,内错角相等,即可求得答案;
(4)由AB∥CD,根据两直线平行,同位角相等,即可求得∠1=∠B,又由三角形外角的性质,即可求得答案.
(5)首先过点E作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,同旁内角互补,两直线平行,内错角相等,即可求得答案;
(6)由AB∥CD,根据两直线平行,内错角相等,两直线平行,同旁内角互补即可求得答案.
解答:
(1)∠E=∠B+∠D.
理由:过点E作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠1=∠B,∠2=∠D,
∴∠BED=∠1+∠2=∠B+∠D.
(2)∠D+∠E+∠B=360°.
理由:过点E作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠B+∠1=180°,∠2+∠D=180°,
∴∠B+∠D+∠BED=∠B+∠1+∠2+∠D=360°.
(3)∠B+∠E-∠D=180°,
理由:过点E作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠B+∠1=180°,∠2=∠D,
∴∠B+∠E+∠D=∠B+∠1+∠2+∠D=180°+2∠D,
∴∠B+∠E-∠D=180°
(4)∠B=∠E+∠D.
理由:∵AB∥CD,
∴∠1=∠B,
∵∠1=∠E+∠D,
∴∠B=∠E+∠D.
(5)∠E+∠D-∠B=180°
理由:过点E作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠B=∠1,∠2+∠D=180°
∴∠B+∠E+∠D=∠B+∠1+∠2+∠D=2∠B+180°,
∠E+∠D-∠B=180°.
(6)∵AB∥CD,
∴∠DEF=∠EFB=60°,∠AEF+∠EFB=180°,
又∵∠DEF=∠D′EF=60°,
∴∠AED′=60°.
故答案为:60°.

(1)∠E=∠B+∠D.
理由:过点E作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠1=∠B,∠2=∠D,
∴∠BED=∠1+∠2=∠B+∠D.
(2)∠D+∠E+∠B=360°.
理由:过点E作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠B+∠1=180°,∠2+∠D=180°,
∴∠B+∠D+∠BED=∠B+∠1+∠2+∠D=360°.
(3)∠B+∠E-∠D=180°,
理由:过点E作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠B+∠1=180°,∠2=∠D,
∴∠B+∠E+∠D=∠B+∠1+∠2+∠D=180°+2∠D,
∴∠B+∠E-∠D=180°
(4)∠B=∠E+∠D.
理由:∵AB∥CD,
∴∠1=∠B,
∵∠1=∠E+∠D,
∴∠B=∠E+∠D.
(5)∠E+∠D-∠B=180°
理由:过点E作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠B=∠1,∠2+∠D=180°
∴∠B+∠E+∠D=∠B+∠1+∠2+∠D=2∠B+180°,
∠E+∠D-∠B=180°.
(6)∵AB∥CD,
∴∠DEF=∠EFB=60°,∠AEF+∠EFB=180°,
又∵∠DEF=∠D′EF=60°,
∴∠AED′=60°.
故答案为:60°.
点评:此题考查了平行线的性质与三角形外角的性质.此题难度不大,解题的关键是注意掌握两直线平行,同位角相等;两直线平行,内错角相等与两直线平行,同旁内角互补定理的应用,注意辅助线的作法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列方程中是一元一次方程的是( )
A、
| ||
| B、x2+5=1 | ||
| C、2x+3y=4 | ||
D、x-2=
|
 如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).
如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0). 如图所示,在平面直角坐标系中,三角形ABC的顶点都在网格点上,其中,点C的坐标为(1,2).
如图所示,在平面直角坐标系中,三角形ABC的顶点都在网格点上,其中,点C的坐标为(1,2). 一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=
一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=