题目内容
如图，一个梯子AB长2.5m，顶端A靠在墙OB上，这时梯子下端A与墙角O距离为0.7m，梯子滑动后停在A′B′的位置上，测得BB′长为0.4m，求梯子底端A滑动了多少米．考点：勾股定理的应用
专题：
分析：要求滑动的距离，显然需要分别放到两个直角三角形中，运用勾股定理求得OA′和OA的长即可．
解答：解：在Rt△AB0中，AB=2.5米，OA=0.7米，故OB=
=2.4米，
在Rt△A′OB′中，AB=A′B′=2.5米，OB′=（2.4-0.4）=2米，故OA′=
=1.5米，
故AA′=OA′-OA=1.5-0.7=0.8米．
所以梯子的底端A滑动了0.8米．
| 2．52-0．72 |
在Rt△A′OB′中，AB=A′B′=2.5米，OB′=（2.4-0.4）=2米，故OA′=
| 2．52-22 |
故AA′=OA′-OA=1.5-0.7=0.8米．
所以梯子的底端A滑动了0.8米．
点评：此题勾股定理的应用，解题中主要注意梯子的长度不变，分别运用勾股定理求得相应的线段的长，然后即可求得结论．
练习册系列答案
相关题目
如图，抛物线y=x2+bx+c经过坐标原点，并与x轴交于点A（2，0）．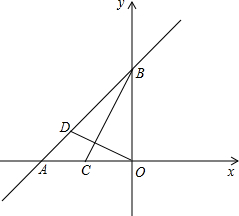
如图，在平面直角坐标系中，直线y=x+4与x轴交于点A，与y轴交于点B，点C（-2，0）．
如图所示，现有边长分别为a、b的正方形、邻边长为a和b（b＞a）的长方形硬纸板若干．
图中的直线为一次函数y=kx+（k-3）的大致图象，试写出一个符合条件的k的值