题目内容
20.先化简$\frac{2}{a-1}$+$\frac{{a}^{2}-4a+4}{{a}^{2}-1}$÷$\frac{a-2}{a+1}$,再选取一个你喜欢的a的值代入求值.分析 先对分式进行化简,再取一个合适的值进行计算即可,但需要注意的是取得的a的值要使原来的式子有意义.
解答 解:$\frac{2}{a-1}$+$\frac{{a}^{2}-4a+4}{{a}^{2}-1}$÷$\frac{a-2}{a+1}$
=$\frac{2}{a-1}+\frac{(a-2)^{2}}{(a+1)(a-1)}×\frac{a+1}{a-2}$
=$\frac{2}{a-1}+\frac{a-2}{a-1}$
=$\frac{2+a-2}{a-1}$
=$\frac{a}{a-1}$.
注意a+1≠0,a-1≠0,a-2≠0,即a≠1,a≠-1,a≠2.
当a=0时,原式=$\frac{a}{a-1}$=$\frac{0}{0-1}$=0.
点评 本题考查分式的化简求值,关键是选取合适的值的时候,选取的a的值要使原来的式子有意义.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
12.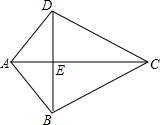 如图,已知AB=AD,BC=CD,AC,BD相交于点E,由这些条件你不能推出结论有( )
如图,已知AB=AD,BC=CD,AC,BD相交于点E,由这些条件你不能推出结论有( )
 如图,已知AB=AD,BC=CD,AC,BD相交于点E,由这些条件你不能推出结论有( )
如图,已知AB=AD,BC=CD,AC,BD相交于点E,由这些条件你不能推出结论有( )| A. | △DAE≌△BAE | B. | ∠CDB=∠DBC | C. | DE=BE | D. | ∠ADB=∠DCA |
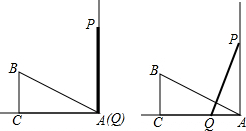 已知墙面与地面成直角,直角△ABC如图放置,BC=3cm,AC=4cm,AB=5cm,一木棒PQ靠在墙上,且PQ=5cm.木棒沿墙面滑下(P向A运动,Q向C运动),P点运动到A点就停止运动,已知P点的运动速度是1cm/s,当P运动1或2s时,△ABC与△PQA全等.
已知墙面与地面成直角,直角△ABC如图放置,BC=3cm,AC=4cm,AB=5cm,一木棒PQ靠在墙上,且PQ=5cm.木棒沿墙面滑下(P向A运动,Q向C运动),P点运动到A点就停止运动,已知P点的运动速度是1cm/s,当P运动1或2s时,△ABC与△PQA全等.