题目内容
12.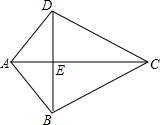 如图,已知AB=AD,BC=CD,AC,BD相交于点E,由这些条件你不能推出结论有( )
如图,已知AB=AD,BC=CD,AC,BD相交于点E,由这些条件你不能推出结论有( )| A. | △DAE≌△BAE | B. | ∠CDB=∠DBC | C. | DE=BE | D. | ∠ADB=∠DCA |
分析 根据全等三角形的判定定理证明△ADC≌△ABC,根据全等三角形的性质和等腰三角形的性质解答.
解答 解:在△ADC和△ABC中,
$\left\{\begin{array}{l}{AD=AB}\\{CD=CB}\\{AC=AC}\end{array}\right.$
∴△ADC≌△ABC,
∴∠DAC=∠BAC,∠ACD=∠ACB,
在△ADE和△ABE中,
$\left\{\begin{array}{l}{AD=AB}\\{∠DAE=∠BAE}\\{AE=AE}\end{array}\right.$,
∴△DAE≌△BAE,故A正确;
∵CD=CB,
∴∠CDB=∠DBC,故B正确;
∵△DAE≌△BAE,
∴DE=BE,故C正确;
∵∠AED=90°,
∴∠ADB+∠DAE=90°,
∵∠ADC≠90°,
∴∠DCA+∠DAC≠90°,
∴∠ADC≠DCA,故D错误;
故选:D.
点评 本题考查的是全等三角形的判定和性质、等腰三角形的判定,掌握全等三角形的判定定理和性质定理、等腰三角形的判定定理是解题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
4.下列式子是最简二次根式的是( )
| A. | $\sqrt{18}$ | B. | $\sqrt{24}$ | C. | $\sqrt{0.5}$ | D. | $\sqrt{6}$ |
1.下表列出了国外几个城市与首都北京的时差(带正号的表示同一时刻比北京时间早的时数,带负号的表示同一时刻比北京时间晚的时数),如北京时间的上午10时,东京时间的10时已过去了1小时,现在已是10+1=11(时).
如果现在是北京时间9月11日15时,那么现在的纽约时间是9月11日2时.
| 城市 | 纽约 | 巴黎 | 东京 | 芝加哥 |
| 时差/时 | -13 | -7 | +1 | -14 |
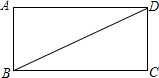 如图,矩形ABCD中,AB=4,BC=8,若以点D为圆心,DA长为半径画弧与以点B为圆心,BD长为半径画弧的交点为P,则点P到AD的距离为8或$\frac{24}{5}$.
如图,矩形ABCD中,AB=4,BC=8,若以点D为圆心,DA长为半径画弧与以点B为圆心,BD长为半径画弧的交点为P,则点P到AD的距离为8或$\frac{24}{5}$.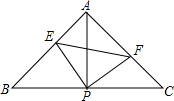 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:①AE=CF; ②△EPF是等腰直角三角形; ③2S四边形AEPF=S△ABC; ④BE+CF=EF.当∠EPF在△ABC内绕顶点P旋转时(点E与A、B重合).上述结论中始终正确的有( )
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:①AE=CF; ②△EPF是等腰直角三角形; ③2S四边形AEPF=S△ABC; ④BE+CF=EF.当∠EPF在△ABC内绕顶点P旋转时(点E与A、B重合).上述结论中始终正确的有( )