题目内容
18．
如图，在△ABC中，AD为∠BAC的平分线，DE⊥AB于点E，DF⊥AC于点F，△ABC的面积是8cm2，AB=5cm，AC=3cm，求DE的长．
分析 根据角平分线性质求出DE=DF，根据三角形面积公式求出即可．
解答 解：∵在△ABC中，AD为∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，
∴DE=DF，
∵△ABC的面积是8cm2，AB=5cm，AC=3cm，
∴$\frac{1}{2}$×5×DE+$\frac{1}{2}$×3×DF=8，
∴DE=DF=2（cm），
即DE的长是2cm．
点评 本题考查了角平分线性质，三角形的面积的应用，解此题的关键是得出关于DE的方程．
练习册系列答案
名校课堂系列答案
相关题目
8．△ABC中，AD是BC边上的高，∠BAD=55°，∠CAD=25°，则∠BAC的度数为（ ）
| A． | 80° | B． | 30° | C． | 100° | D． | 80°或30° |
如图①，有一池塘，要测池塘两端A、B的距离，可先在平地上取一个点C，从点C不经过池塘可以直接到达点A和B，连接AC并延长到点D，使CD=CA，连接BC并延长到点E，使CE=CB，连接DE．
如图，在△ABC中，已知AD=DE，AB=BE，∠A=85°，∠C=45°，则∠CDE=40°．
7．
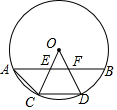如图所示，在⊙O中，A，C，D，B是⊙O上四点，OC，OD交AB于点E，F，且AE=FB，下列结论：①OE=OF；②AC=CD=DB；③CD∥AB；④$\widehat{AC}$=$\widehat{BD}$，其中正确的有（ ）
如图所示，在⊙O中，A，C，D，B是⊙O上四点，OC，OD交AB于点E，F，且AE=FB，下列结论：①OE=OF；②AC=CD=DB；③CD∥AB；④$\widehat{AC}$=$\widehat{BD}$，其中正确的有（ ）| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
8．
如图，在△ABC中，∠A=60°，∠C=90°，CD是∠ACB的平分线，则∠BDC等于（ ）
如图，在△ABC中，∠A=60°，∠C=90°，CD是∠ACB的平分线，则∠BDC等于（ ）| A． | 75° | B． | 95° | C． | 105° | D． | 110° |