题目内容
9.用适当的方法解一元二次方程:(1)x2+3x-4=0
(2)3x(x-2)=2(2-x)
(3)(x+8)(x+1)=-12.
分析 (1)因式分解法求解可得;
(2)因式分解法求解可得;
(3)整理成一般式后,因式分解法求解可得.
解答 解:(1)∵(x-1)(x+4)=0,
∴x-1=0或x+4=0,
解得:x=1或x=-4;
(2)∵3x(x-2)+2(x-2)=0,
∴(x-2)(3x+2)=0,
∴x-2=0或3x+2=0,
解得:x=2或x=-$\frac{2}{3}$;
(3)整理成一般式可得x2+9x+20=0,
∵(x+4)(x+5)=0,
∴x+4=0或x+5=0,
解得:x=-4或x=-5.
点评 本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
20.下列各项中,去括号正确的是( )
| A. | x2-2(2x-y+2)=x2-4x-2y+4 | B. | -3(m+n)-mn=-3m+3n-mn | ||
| C. | -(5x-3y)+4(2xy-y2)=-5x+3y+8xy-4y2 | D. | ab-5(-a+3)=ab+5a-3 |
14.已知一元二次方程x2-4x+3=0两根为x1、x2,则x1•x2=( )
| A. | 3 | B. | 4 | C. | -4 | D. | -3 |
19. 如图所示,在数轴上点A表示的数可能是( )
如图所示,在数轴上点A表示的数可能是( )
 如图所示,在数轴上点A表示的数可能是( )
如图所示,在数轴上点A表示的数可能是( )| A. | -3.7 | B. | -3.2 | C. | -2.7 | D. | -2.2 |
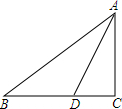 如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=12cm,BD=9cm,则点D到AB的距离是3cm.
如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=12cm,BD=9cm,则点D到AB的距离是3cm. 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC的面积是8cm2,AB=5cm,AC=3cm,求DE的长.
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC的面积是8cm2,AB=5cm,AC=3cm,求DE的长.