Question

7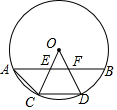．如图所示，在⊙O中，A，C，D，B是⊙O上四点，OC，OD交AB于点E，F，且AE=FB，下列结论：①OE=OF；②AC=CD=DB；③CD∥AB；④$\widehat{AC}$=$\widehat{BD}$，其中正确的有（　　）

• A． 4个
• B． 3个
• C． 2个
• D． 1个

Answer 1

分析 连接OA，OB，可以利用SAS判定△OAE≌△OBF，根据全等三角形的对应边相等，可得到OE=OF，判断①正确；由全等三角形的对应角相等，可得到∠AOE=∠BOF，即∠AOC=∠BOD，根据圆心角、弧、弦的关系定理得出$\widehat{AC}=\widehat{BD}$，判断④正确；连结AD．由$\widehat{AC}=\widehat{BD}$，根据圆周角定理得出∠BAD=∠ADC，则CD∥AB，③选项正确；由∠BOD=∠AOC不一定等于∠COD，得出弧AC=弧BD不一定等于弧CD，那么AC=BD不一定等于CD，判断②不正确．

解答 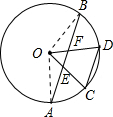解：连接OA，OB，
∵OA=OB，
∴∠OAB=∠OBA．
在△OAE与△OBF中，$\left\{\begin{array}{l}{OA=OB}&{\;}\\{∠OAE=∠OBF}&{\;}\\{AE=BF}&{\;}\end{array}\right.$，
∴△OAE≌△OBF（SAS），
∴OE=OF，故①正确；
∠AOE=∠BOF，即∠AOC=∠BOD，
∴$\widehat{AC}=\widehat{BD}$，故④正确；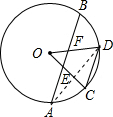
连结AD．
∵$\widehat{AC}=\widehat{BD}$，
∴∠BAD=∠ADC，
∴CD∥AB，故③正确；
∵∠BOD=∠AOC不一定等于∠COD，
∴弧AC=弧BD不一定等于弧CD，
∴AC=BD不一定等于CD，
故②不正确．
正确的有3个，故选B．

点评 本题考查了全等三角形的判定与性质，圆心角、弧、弦的关系定理，圆周角定理，平行线的判定，难度适中．准确作出辅助线利用数形结合思想是解题的关键．