题目内容
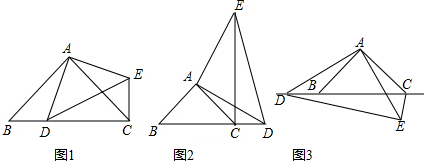
3. 如图①,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB,连接DE.
如图①,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB,连接DE.(1)量出DE的长就是A、B的距离,为什么?
(2)请你利用图②设计一个测池塘两端A、B的距离的方案.
要求:①画出图形;
②写出方案,给出简要证明;
③给出的方案不能用到图①的方法.
分析 (1)借助△ACB≌△DCE用SAS证明,(其中两边已知,角为对顶角),寻找所求线段与已知线段之间的等量关系;
(2)直接利用等腰直角三角形的性质得出符合题意的答案.
解答 解:(1)在△ACB与△DCE中,
∵$\left\{\begin{array}{l}{CA=CD}\\{∠ACB=∠DCE}\\{CB=CE}\end{array}\right.$,
∴△ACB≌△DCE(SAS),
∴AB=DE,
即DE的长就是A、B的距离.
(2)答案不唯一:
如图②,作∠CAB=90°,∠ABC=45°,
则△ABC是等腰直角三角形,测量AC的长,就是池塘两端A,B的距离.
点评 此题考查了应用设计与作图,在实际生活中,对于难以实地测量的线段,常常通过两个全等三角形,转化需要测量的线段到易测量的边上或者已知边上来,从而求解.

练习册系列答案
相关题目
13.下列说法正确的是( )
| A. | b的指数是0 | B. | b没有系数 | C. | a是单项式 | D. | -3是一次单项式 |
14.已知一元二次方程x2-4x+3=0两根为x1、x2,则x1•x2=( )
| A. | 3 | B. | 4 | C. | -4 | D. | -3 |
11.一个正多边形的内角和是540°,这个多边形每个内角的度数是( )
| A. | 108° | B. | 118° | C. | 98° | D. | 72° |
15.M是线段AB中点,下列说法中:①AM+MB=AB;②AM=BM;③AB=2BM;④AM=2BM.正确的是( )
| A. | ①② | B. | ①②③ | C. | ③④ | D. | ①④ |
 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC的面积是8cm2,AB=5cm,AC=3cm,求DE的长.
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC的面积是8cm2,AB=5cm,AC=3cm,求DE的长.