题目内容
16.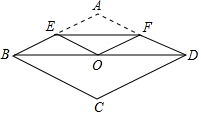 如图,将边长为4的菱形ABCD纸片折叠,使点A恰好落在对角线的交点O处,若折痕EF=2$\sqrt{3}$,则∠A=( )
如图,将边长为4的菱形ABCD纸片折叠,使点A恰好落在对角线的交点O处,若折痕EF=2$\sqrt{3}$,则∠A=( )| A. | 120° | B. | 100° | C. | 60° | D. | 30° |
分析 连接AC,根据菱形的性质得出AC⊥BD,根据折叠得出EF⊥AC,EF平分AO,得出EF∥BD,得出EF为△ABD的中位线,根据三角形中位线定理求出BD的长,进而可得到BO的长,由勾股定理可求出AO的长,则∠ABO可求出,继而∠BAO的度数也可求出,再由菱形的性质可得∠A=2∠BAO.
解答 解:
连接AC,
∵四边形ABCD是菱形,
∴AC⊥BD,
∵A沿EF折叠与O重合,
∴EF⊥AC,EF平分AO,
∵AC⊥BD,
∴EF∥BD,
∴E、F分别为AB、AD的中点,
∴EF为△ABD的中位线,
∴EF=BD,
∴BD=2EF=4$\sqrt{3}$,
∴BO=2$\sqrt{3}$,
∴AO=$\sqrt{A{B}^{2}-B{O}^{2}}$=2,
∴AO=$\frac{1}{2}$AB,
∴∠ABO=30°,
∴∠BAO=60°,
∴∠BAD=120°.
故选A.
点评 本题考查了折叠的性质、菱形的性质、三角形中位线定理以及勾股定理的运用;熟练掌握菱形的性质和翻折变换的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
7.在以下一列数3,3,5,6,7,8中,中位数是( )
| A. | 3 | B. | 5 | C. | 5.5 | D. | 6 |
19.|-5+2|=( )
| A. | -7 | B. | 7 | C. | -3 | D. | 3 |
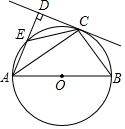 如图,AB为⊙O的直径,C为⊙O上一点,AD与过点C的切线互相垂直,垂足为点D,AD交⊙O于点E,连接CE,CB.
如图,AB为⊙O的直径,C为⊙O上一点,AD与过点C的切线互相垂直,垂足为点D,AD交⊙O于点E,连接CE,CB.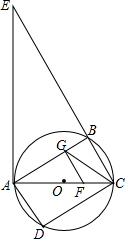 如图,四边形ABCD内接于圆O,∠BAD=90°,AC为直径,过点A作圆O的切线交CB的延长线于点E,过AC的三等分点F(靠近点C)作CE的平行线交AB于点G,连结CG.
如图,四边形ABCD内接于圆O,∠BAD=90°,AC为直径,过点A作圆O的切线交CB的延长线于点E,过AC的三等分点F(靠近点C)作CE的平行线交AB于点G,连结CG.