题目内容
1.在平面直角坐标系中,点P(x,y)经过某种变换后得到点P'(-y+1,x+2),我们把点P'(-y+1,x+2)叫做点P(x,y)的终结点.已知点P1的终结点为P2,点P2的终结点为P3,点P3的终结点为P4,这样依次得到P1、P2、P3、P4、…Pn、…,若点P1的坐标为(2,0),则点P2017的坐标为(2,0).分析 求得点P2、P3、P4、P5的值,即可发现其中规律,即可解题.
解答 解:P1 坐标为(2,0),则P2坐标为(1,4),P3坐标为(-3,3),P4坐标为(-2,-1),P5坐标为(2,0),
∴Pn的坐标为(2,0),(1,4),(-3,3),(-2,-1)循环,
∵2017=2016+1=4×504+1,
∴P2017 坐标与P1点重合,
故答案为(2,0).
点评 本题考查了学生发现点的规律的能力,本题中找到Pn坐标得规律是解题的关键.

练习册系列答案
相关题目
11.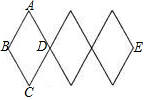 如图,是伸缩衣架的实物图和示意图,它是由4条短木棒和4条长木棒组成的三个全等的菱形,其中AB=20cm,当∠BAD由60°变为120°时,衣架的总长度BE拉长了( )
如图,是伸缩衣架的实物图和示意图,它是由4条短木棒和4条长木棒组成的三个全等的菱形,其中AB=20cm,当∠BAD由60°变为120°时,衣架的总长度BE拉长了( )
 如图,是伸缩衣架的实物图和示意图,它是由4条短木棒和4条长木棒组成的三个全等的菱形,其中AB=20cm,当∠BAD由60°变为120°时,衣架的总长度BE拉长了( )
如图,是伸缩衣架的实物图和示意图,它是由4条短木棒和4条长木棒组成的三个全等的菱形,其中AB=20cm,当∠BAD由60°变为120°时,衣架的总长度BE拉长了( )| A. | (20$\sqrt{3}$-20)cm | B. | (40$\sqrt{3}$-40)cm | C. | (60-30$\sqrt{3}$)cm | D. | (60$\sqrt{3}$-60)cm |
16.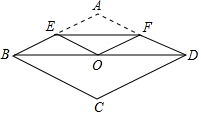 如图,将边长为4的菱形ABCD纸片折叠,使点A恰好落在对角线的交点O处,若折痕EF=2$\sqrt{3}$,则∠A=( )
如图,将边长为4的菱形ABCD纸片折叠,使点A恰好落在对角线的交点O处,若折痕EF=2$\sqrt{3}$,则∠A=( )
 如图,将边长为4的菱形ABCD纸片折叠,使点A恰好落在对角线的交点O处,若折痕EF=2$\sqrt{3}$,则∠A=( )
如图,将边长为4的菱形ABCD纸片折叠,使点A恰好落在对角线的交点O处,若折痕EF=2$\sqrt{3}$,则∠A=( )| A. | 120° | B. | 100° | C. | 60° | D. | 30° |
4.下列各数中,无理数的是( )
| A. | 0 | B. | -1 | C. | $\sqrt{2}$ | D. | 1.414 |
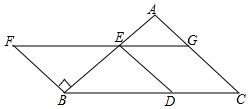 如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.
如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.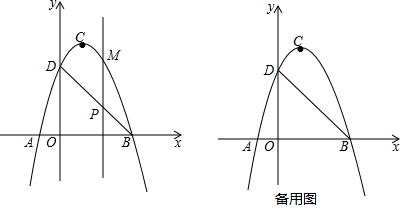
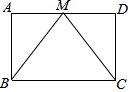 已知:如图,M是矩形ABCD的边AD的中点,求证:MB=MC.
已知:如图,M是矩形ABCD的边AD的中点,求证:MB=MC. 已知一次函数y=2x+a与y=-x+b的图象都经过A(-2,0),且与y轴分别交于B、C两点.
已知一次函数y=2x+a与y=-x+b的图象都经过A(-2,0),且与y轴分别交于B、C两点.