��Ŀ����
4����ͼ����һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü���ƽ���ֳ��Ŀ�С�����Σ�Ȼ��ͼ�ڵ���״Χ��һ�������Σ���1��ͼ���е���Ӱ�������Ϊ��m+n��2-4mn��m-n��2��
��2���۲�ͼ�ڣ�����д����������ʽ��m+n��2����m-n��2��mn֮��ĵ�����ϵ�ǣ�m+n��2-4mn=��m-n��2��
��3��ʵ����������������ʽ������ͼ�ε��������ʾ����ͼ�ۣ�����ʾ�ˣ�2m+n����m+n��=2m2+3mn+n2��
��4���Ի���һ������ͼ�Σ�ʹ��������ܱ�ʾ��m+n����m+3n��=m2+4mn+3n2������ͼ�б����Ӧ�ij��ȣ�
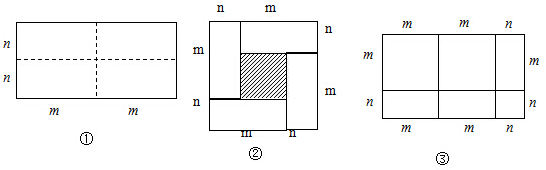
���� ��1������ͼ�α�ʾ����Ӱ���ֵ�������ɣ�
��2�����ݣ�1���еĽ���ó����ɣ�
��3�����ݴ���������ڳ����Կ���5����������͵����ֲ�ͬ�㷨���г���ʽ��
��4��������m+n�Ϳ�m+3n�ľ��Σ��ٷֳ�8�����μ��ɣ�
��� �⣺��1��ͼ������Ӱ���ֵ����Ϊ��m+n��2-4mn��m-n��2��
�ʴ�Ϊ����m+n��2-4mn��m-n��2��
��2����������ʽ��m+n��2����m-n��2��mn֮��ĵ�����ϵ�ǣ�m+n��2-4mn=��m-n��2��
�ʴ�Ϊ����m+n��2-4mn=��m-n��2��
��3��ͼ�۱�ʾ�Ĺ�ϵʽΪ����2m+n����m+n��=2m2+3mn+n2��
�ʴ�Ϊ����2m+n����m+n��=2m2+3mn+n2��
��4����ͼ��ʾ�� ��
��
���� ���⿼������ȫƽ����ʽ�ļ��α��������ڻ����⣬ע����ϸ�۲�ͼ�Σ���ʾ����ͼ�ε�����ǹؼ���

��ϰ��ϵ�д�
 �ŵ������ϵ�д�
�ŵ������ϵ�д� 53������ϵ�д�
53������ϵ�д�
�����Ŀ
14�����м����У���ȷ���ǣ�������
| A�� | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B�� | 3$\sqrt{2}$-$\sqrt{2}$=3 | C�� | $\sqrt{4\frac{1}{4}}$=2$\frac{1}{2}$ | D�� | $\sqrt{��-3��^{2}}$=3 |
 ��֪a��b��c�������ϵ�λ����ͼ������|a|+|c-b|-|c|��
��֪a��b��c�������ϵ�λ����ͼ������|a|+|c-b|-|c|�� ��ͼ����֪��P��������ABCD�ĶԽ���BD�ϵ�һ�㣬��BP=BC�����PCD�Ķ�����22.5�㣮
��ͼ����֪��P��������ABCD�ĶԽ���BD�ϵ�һ�㣬��BP=BC�����PCD�Ķ�����22.5�㣮 ��ͼ��ֱ��y=kx+b���������ཻ�ڵ�M��3��0����N��0��4����
��ͼ��ֱ��y=kx+b���������ཻ�ڵ�M��3��0����N��0��4����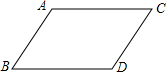 ��ͼ������Ϊ4cm���߶�AB���ŵ�A����C�ķ���ƽ��6cm�õ��߶�CD����ô�ı���ABDC���ܳ���20cm��
��ͼ������Ϊ4cm���߶�AB���ŵ�A����C�ķ���ƽ��6cm�õ��߶�CD����ô�ı���ABDC���ܳ���20cm��