题目内容
20．
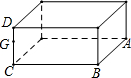如图，地面上有一立方体物块宽AB=4cm，长BC=8cm，CD上的点G距地面的高CG=5cm，地面上一只蚂蚁从A处爬到G处，要爬行的最短路程是（ ）| A． | 6cm | B． | $4+\sqrt{89}$cm | C． | 13cm | D． | 17cm |
分析 要求不在同一平面内的两点间的最短距离，首先要把两点所在的两个平面展开到一个平面内，然后根据题意确定数据，再根据勾股定理即可求解．
解答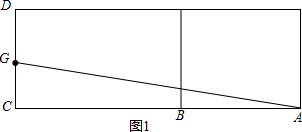 
解：如图1所示，连接AG，则AG的长即为A处到G处的最短路程．
在Rt△ACG中，
∵AC=AB+BC=12cm，CG=5cm，
∴AG=$\sqrt{A{C}^{2}+C{G}^{2}}$=$\sqrt{1{2}^{2}+{5}^{2}}$=13（cm）．
∴需要爬行的最短路径是13cm．
故选C．
点评 本题的是平面展开-最短路径问题，解答此类问题时要先根据题意把立体图形展开成平面图形后，再确定两点之间的最短路径．一般情况是两点之间，线段最短．在平面图形上构造直角三角形解决问题．
练习册系列答案
相关题目
10．某商场计划购进甲，乙两种节能灯共1200只，这两种节能灯的进价和售价如下表：
（1）求甲，乙两种节能灯各进货多少时，使进货款恰好为46 000元；
（2）应如何进货，使销售完节能灯时，商场获得的利润恰好是进货价的30%，此时利润为多少？
| 进价（元/只） | 售价（元/只） | |
| 甲型 | 25 | 30 |
| 乙型 | 45 | 60 |
（2）应如何进货，使销售完节能灯时，商场获得的利润恰好是进货价的30%，此时利润为多少？
8．下列事件中为必然事件的是（ ）
| A． | 从一定高度落下的图钉落地后顶尖朝上 | |
| B． | 打开数学课本时刚好翻到第60页 | |
| C． | 早晨太阳一定从东方升起 | |
| D． | 今年14岁的小明一定是初中学生 |
15．为开展阳光体育活动，某校组织了八年级五个班的足球赛，为更清楚地表示出首轮比赛中各班的总进球数，我们最好选择（ ）
| A． | 折线统计图 | B． | 条形统计图 | C． | 扇形统计图 | D． | 以上三种都可以 |
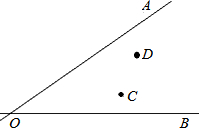如图所示，成纪大道与天北高速在七里墩相交于点O，在∠AOB的内部有工厂C和D，现要建一个货场P，使P到OA和OB的距离相等，且使PC=PD，用尺规作出P点的位置．（不写作法，保留作图痕迹）
12．
如图，DE∥BC，且AD=4，DB=2，DE=3.5，则BC的长度为（ ）
如图，DE∥BC，且AD=4，DB=2，DE=3.5，则BC的长度为（ ）| A． | 5.5 | B． | 5.25 | C． | 6.5 | D． | 7 |
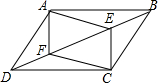如图，点B，E，F，D在一条直线上，且DE=BF，点A，C在直线BD的两側，且AB=CD，AE=CF．连接AD，AF，CB，CE，则图中的全等三角形共有（ ）