题目内容
4.分解因式:(1)(xy+1)(x+1)(y+1)+xy
(2)(a-b)(3a+b)2+(a+3b)2(b-a)
分析 (1)把xy+1当一个整体,去括号再因式分解即可;
(2)把后面的b-a换成-(a-b),再提公因式,再利用平方差分解即可.
解答 解:
(1)(xy+1))(x+1)(y+1)+xy
=(xy+1)(xy+x+y+1)+xy
=(xy+1)2+(xy+1)(x+y)+xy
=(xy+1+x)(xy+1+y);
(2)(a-b)(3a+b)2+(a+3b)2(b-a)
=(a-b)(3a+b)2-(a+3b)2(a-b)
=(a-b)[(3a+b)2-(a+3b)2]
=(a-b)[(3a+b)+(a+3b)][(3a+b)-(a+3b)]
=(a-b)(3a+b+a+3b)(3a+b-a-3b)
=(a-b)(4a+4b)(2a-2b)
=8(a-b)2(a+b).
点评 本题主要考查因式分解的方法,掌握提公因式法和公式法是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列方程:①x2=0,②$\frac{1}{x^2}$-2=0,③2x2+3x=(1+2x)(2+x),④$\frac{{2{x^3}}}{x}$-8x+1=0中,一元二次方程的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.下列说法中,正确的是( )
| A. | 全等图形是形状相同的两个图形 | |
| B. | 全等三角形是指面积相同的两个三角形 | |
| C. | 等边三角形都是全等三角形 | |
| D. | 全等图形的周长、面积都相等 |
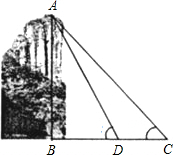 如图,为测得峰顶A到河面B的高度,当游船行至C处时测得峰顶A的仰角为45°,前进20米至D处时测得峰顶A的仰角为60°(此时C、D、B三点在同一直线上),求峰顶A到河面B的高度.(精确到0.1m,$\sqrt{2}$≈1.41,$\sqrt{3}$=1.73)
如图,为测得峰顶A到河面B的高度,当游船行至C处时测得峰顶A的仰角为45°,前进20米至D处时测得峰顶A的仰角为60°(此时C、D、B三点在同一直线上),求峰顶A到河面B的高度.(精确到0.1m,$\sqrt{2}$≈1.41,$\sqrt{3}$=1.73) 如图所示,根据图形把多项式a2+5ab+4b2因式分解=(a+b)(a+4b).
如图所示,根据图形把多项式a2+5ab+4b2因式分解=(a+b)(a+4b).