题目内容
 如图,△ABC中,∠A=36°,∠C=72°,∠DBC=36°.
如图,△ABC中,∠A=36°,∠C=72°,∠DBC=36°.(1)求∠1的度数;
(2)求证:BC=BD=AD.
考点:等腰三角形的判定与性质
专题:
分析:(1)由∠C=72゜,∠A=∠DBC=36゜,根据三角形内角和定理,可求得∠ABD=∠A=36°;
(2)进一步求出∠ABC=∠BCD=∠BDC=72°,得出BD=BC,再由∠ABD=∠A得出BD=AD,继而求得答案.
(2)进一步求出∠ABC=∠BCD=∠BDC=72°,得出BD=BC,再由∠ABD=∠A得出BD=AD,继而求得答案.
解答:(1)解:在△ABC中,
∠ABC=180°-∠A-∠C=72°,
∴∠1=∠ABC-∠DBC=36°;
(2)证明:在△BCD中,
∠2=180°-∠DBC-∠C=72°,
∴∠2=∠C,
∴BD=BC,
又∠ABD=∠A,
∴BD=AD,
∴BC=BD=AD.
∠ABC=180°-∠A-∠C=72°,
∴∠1=∠ABC-∠DBC=36°;
(2)证明:在△BCD中,
∠2=180°-∠DBC-∠C=72°,
∴∠2=∠C,
∴BD=BC,
又∠ABD=∠A,
∴BD=AD,
∴BC=BD=AD.
点评:此题考查三角形的内角和定理,等腰三角形的判定与性质,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 如图,已知数轴上有A、B、C三个点,它们表示的数分别是-24,-10,10.
如图,已知数轴上有A、B、C三个点,它们表示的数分别是-24,-10,10.
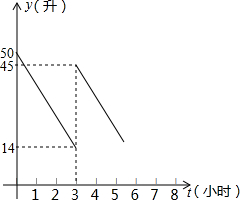 汽车出发前油箱有油50L,行驶若干小时后,在加油站加油若干升.图象表示的是从出发后,油箱中剩余油量y(L)与行驶时间t(h)之间的关系.
汽车出发前油箱有油50L,行驶若干小时后,在加油站加油若干升.图象表示的是从出发后,油箱中剩余油量y(L)与行驶时间t(h)之间的关系. 如图,在△ABC与△DEF中,如果AB=DE,BE=CF,只要加上
如图,在△ABC与△DEF中,如果AB=DE,BE=CF,只要加上