题目内容
18.抛物线y=-x2+(m-1)x+m与y轴交于点(0,3)(1)求m的值;
(2)求它与x轴的交点坐标;
(3)x取什么值时?抛物线在x轴上方.
分析 (1)把已知点的坐标代入抛物线解析式可求得m的值;
(2)令y=0可得到关于x的一元二次方程,则可求得与x轴的交点坐标;
(3)由抛物线的开口方向及与x轴的交点坐标可求得答案.
解答 解:
(1)∵抛物线y=-x2+(m-1)x+m与y轴交于点(0,3),
∴m=3;
(2)由(1)可知抛物线解析式为y=-x2+2x+3,
令y=0可得-x2+2x+3=0,解得x=-1或x=3,
∴抛物线与x轴的交点坐标为(-1,0)或(3,0);
(3)∵y=-x2+2x+3,
∴抛物线开口向下,且与x轴的交点坐标为(-1,0)或(3,0),
∴当-1<x<3时,抛物线在x轴上方.
点评 本题主要考查二次函数图象与性质,求得抛物线解析式是解题的关键.

练习册系列答案
相关题目
3.用平面去截一个立方体,截面不可能是( )
| A. | 正方形 | B. | 五边形 | C. | 六边形 | D. | 七边形 |
10.已知某水库的警戒水位为18.8m,值班人员记录了某一周内的水位变化情况,如下表:(单位:m,上周末刚好到达警戒水位,取警戒水位为0,“+”表示水位比前一天升高,“-”表示水位比前一天降低)
(1)本周内哪一天水位最高?哪一天水位最低?它们与警戒水位相差多少?
(2)若超过警戒水位1.5m时就应该开闸放水,以确保大坝安全,本周水库需开闸放水吗?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 变化情况(m) | +0.3 | +0.4 | -0.2 | +0.3 | +0.4 | -0.1 | -0.5 |
(2)若超过警戒水位1.5m时就应该开闸放水,以确保大坝安全,本周水库需开闸放水吗?
 如图,点D、E、F分别是BC、AD、BC的中点,若△ABC的面积是20,则△BEF的面积为5.
如图,点D、E、F分别是BC、AD、BC的中点,若△ABC的面积是20,则△BEF的面积为5. 如图,A、C、D为⊙O上的点,∠D=35°,则∠AOC=70°.
如图,A、C、D为⊙O上的点,∠D=35°,则∠AOC=70°.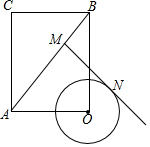 如图,在矩形AOBC中,AO=3,BO=4,⊙O的半径为1,点M是矩形对角线AB边上的动点,过点M做⊙O的一条切线MN,切点为N,则切线长MN的最小值是$\frac{\sqrt{119}}{5}$.
如图,在矩形AOBC中,AO=3,BO=4,⊙O的半径为1,点M是矩形对角线AB边上的动点,过点M做⊙O的一条切线MN,切点为N,则切线长MN的最小值是$\frac{\sqrt{119}}{5}$.