题目内容
 已知抛物线y=x2+bx+c,若抛物线经过点(1,-6),(-1,0)
已知抛物线y=x2+bx+c,若抛物线经过点(1,-6),(-1,0)(1)求抛物线解析式;
(2)通过配方求此抛物线的顶点坐标和对称轴;
(3)在如图所示的坐标系中画出(1)中的函数图象;
(4)根据图象指出,当x为何值时,抛物线在x轴上方?当x为何值时y的值随x的增大而增大?
考点:待定系数法求二次函数解析式,二次函数的图象,二次函数的性质
专题:计算题
分析:(1)将(1,-6)和(-1,0)代入抛物线解析式,得到关于b与c的方程组,求出方程组的解得到b与c的值,即可确定出抛物线解析式;
(2)利用配方法将抛物线解析式化为顶点形式,令平方的底数等于0,求出顶点横坐标,将横坐标代入抛物线解析式中求出y的值,确定出顶点纵坐标,即可确定出抛物线顶点坐标和对称轴;
(3)由确定出的抛物线解析式,利用列表,描点,连线的步骤,即可画出抛物线的图象;
(4)令抛物线解析式中y=0,得出关于x的方程,求出方程的解得出抛物线与x轴交点的坐标,由函数图象,即可得出抛物线图象在x轴上方时x的范围,由抛物线开口向上,及抛物线的对称轴可得出当x在对称轴右边时,y随x的增大而增大.
(2)利用配方法将抛物线解析式化为顶点形式,令平方的底数等于0,求出顶点横坐标,将横坐标代入抛物线解析式中求出y的值,确定出顶点纵坐标,即可确定出抛物线顶点坐标和对称轴;
(3)由确定出的抛物线解析式,利用列表,描点,连线的步骤,即可画出抛物线的图象;
(4)令抛物线解析式中y=0,得出关于x的方程,求出方程的解得出抛物线与x轴交点的坐标,由函数图象,即可得出抛物线图象在x轴上方时x的范围,由抛物线开口向上,及抛物线的对称轴可得出当x在对称轴右边时,y随x的增大而增大.
解答: 解:(1)将(1,-6)和(-1,0)代入y=x2+bx+c中,得
解:(1)将(1,-6)和(-1,0)代入y=x2+bx+c中,得
,
解得:
,
则抛物线解析式为y=x2-3x-4;
(2)y=x2-3x-4=x2-3x+
-
-4=(x-
)2-
,
则抛物线的顶点坐标为(
,-
),对称轴为直线x=
;
(3)列表如下:
描点:如图所示;
连线,如图所示:
(4)令y=0,得到x2-3x-4=0,解得x=-1或x=4,
∴抛物线与x轴的交点为(-1,0)和(4,0),
∴由图象可得当x<-1或x>4时,抛物线在x轴上方,
又抛物线对称轴为直线x=
,
∴当x>
时,y随x的增大为增大.
 解:(1)将(1,-6)和(-1,0)代入y=x2+bx+c中,得
解:(1)将(1,-6)和(-1,0)代入y=x2+bx+c中,得
|
解得:
|
则抛物线解析式为y=x2-3x-4;
(2)y=x2-3x-4=x2-3x+
| 9 |
| 4 |
| 9 |
| 4 |
| 3 |
| 2 |
| 25 |
| 4 |
则抛物线的顶点坐标为(
| 3 |
| 2 |
| 25 |
| 4 |
| 3 |
| 2 |
(3)列表如下:
| x | 0 | 1 |
|
2 | 3 | ||
| y | -4 | -6 | -
|
-6 | -4 |
连线,如图所示:
(4)令y=0,得到x2-3x-4=0,解得x=-1或x=4,
∴抛物线与x轴的交点为(-1,0)和(4,0),
∴由图象可得当x<-1或x>4时,抛物线在x轴上方,
又抛物线对称轴为直线x=
| 3 |
| 2 |
∴当x>
| 3 |
| 2 |
点评:此题考查了待定系数法确定抛物线解析式,函数图象的画法,以及二次函数的图象与性质,利用了数形结合的思想,待定系数法是数学中重要的思想方法,学生做题时注意灵活运用.

练习册系列答案
相关题目
 如图,在矩形ABCD中,E是BC中点,DE⊥AC,则CD:AD为( )
如图,在矩形ABCD中,E是BC中点,DE⊥AC,则CD:AD为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
已知关于x的一元二次方程2x2+4xsinα+1=0有两个相等的实数根,则锐角α的度数为( )
| A、30° | B、45° |
| C、60° | D、90° |
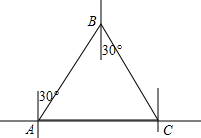 海上有两个观测站A、B,测得B站在A站AB=30海里.一艘船C,在A站的正东,在B站的南偏东30°处.此时船正向正北方向航行,半小时后达到D处,此时测得船在A站北偏东60°方向,在B站南偏东75°方向.
海上有两个观测站A、B,测得B站在A站AB=30海里.一艘船C,在A站的正东,在B站的南偏东30°处.此时船正向正北方向航行,半小时后达到D处,此时测得船在A站北偏东60°方向,在B站南偏东75°方向.