题目内容
15.从-3,-1,-$\frac{1}{2}$,1,2这五个数中,随机抽取一个数,作为抛物线y=x2+2mx+m中m的值,恰好使所得抛物线的顶点在第四象限概率为$\frac{3}{5}$.分析 确定使函数的图象顶点在第四象限的m的值,找到同时满足两个条件的m的值即可.
解答 解:因为抛物线y=x2+2mx+m的顶点在第四象限,
可得:$\left\{\begin{array}{l}{-m>0}\\{-{m}^{2}+m<0}\end{array}\right.$,
解得:m<0,
所以恰好使所得抛物线的顶点在第四象限概率为$\frac{3}{5}$,
故答案为:$\frac{3}{5}$
点评 此题考查了概率公式的应用.注意用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
5.计算:1+(-2)+(+3)+(-4)+(+5)+(-6)…(+99)+(-100)的结果是( )
| A. | 0 | B. | -1 | C. | -50 | D. | 51 |
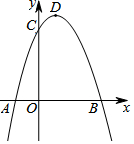 已知二次函数y=ax2+bx-3a经过点A(-1,0),C(0,3),与x轴交于另一点B,抛物线的顶点为D.
已知二次函数y=ax2+bx-3a经过点A(-1,0),C(0,3),与x轴交于另一点B,抛物线的顶点为D. 如图,已知AB=AC,∠A=40°,AB=10,DC=3,AB的垂直平分线MN交AC于点D,则∠DBC=30度,BD=7.
如图,已知AB=AC,∠A=40°,AB=10,DC=3,AB的垂直平分线MN交AC于点D,则∠DBC=30度,BD=7.
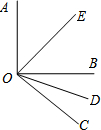 如图所示,OE,OD分别平分∠AOB和∠BOC,且∠AOB=90°,如果∠BOC=40°,求∠EOD的度数.
如图所示,OE,OD分别平分∠AOB和∠BOC,且∠AOB=90°,如果∠BOC=40°,求∠EOD的度数.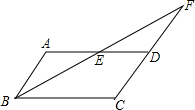 如图,在?ABCD中,点E是AD的中点,BE的延长线与CD的延长线相交于点F.
如图,在?ABCD中,点E是AD的中点,BE的延长线与CD的延长线相交于点F.