题目内容
4.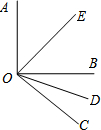 如图所示,OE,OD分别平分∠AOB和∠BOC,且∠AOB=90°,如果∠BOC=40°,求∠EOD的度数.
如图所示,OE,OD分别平分∠AOB和∠BOC,且∠AOB=90°,如果∠BOC=40°,求∠EOD的度数.
分析 根据图示找出所求各角之间的关系,∠EOD=∠EOB+∠BOD,利用角平分线的定义,求出这个角的度数,即可求结果.
解答 解:∵OE,OD分别平分∠AOB和∠BOC,且∠AOB=90°,∠BOC=40°,
∴∠EOB=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×90°=45°,
∠BOD=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×40°=20°,
∴∠EOD=∠EOB+∠BOD=65°.
点评 本题考查了角的计算及角平分线的定义,首先确定各角之间的关系,利用角平分线的性质来求.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
19.将抛物线y=(x-1)2+2向右平移3个单位长度,再向上平移2个单位长度后,得到的抛物线的解析式为( )
| A. | y=(x-4)2+4 | B. | y=(x-4)2+6 | C. | y=(x+2)2+6 | D. | y=(x-1)2+4 |
9.y=x2-2x-3的顶点坐标和对称轴( )
| A. | (-1,-4),直线x=-1 | B. | (1,-4),直线x=1 | C. | (-1,4),直线x=-1 | D. | (1,4),直线x=1 |
14.西安铁一中滨河学校为了提高五人小组合作热情并促进学生平时对各科核心知识的落实,自建校以来有一个教学特色即每周每天随机从各班选一个小组进行一科的抽检.已知初二一数学老师所带班级的两个小组共10名学生的一次数学抽检成绩平均分是73分,设这个班10名学生抽检成绩的中位数为b分,下表是具体分数统计表:
则x,b的值分别是( )
| 成绩(分) | 50 | 60 | 70 | 80 | 90 |
| 人数(人) | 1 | 2 | x | y | 2 |
| A. | 3,70 | B. | 3,75 | C. | 2,70 | D. | 2,75 |
 在长为10m,宽为8m的长方形空地中,沿平行于长方形各边的方向分割出三个全等的小长方形花圃,其示意图如图所示.则小长方形花圃的长和宽分别是多少?
在长为10m,宽为8m的长方形空地中,沿平行于长方形各边的方向分割出三个全等的小长方形花圃,其示意图如图所示.则小长方形花圃的长和宽分别是多少?