题目内容
一个不透明的布袋里装有3个球，其中2个红球，1个白球，它们除颜色外其余都相同．
（1）摸出1个球，记下颜色后放回，并搅匀，再摸出1个球，求两次摸出的球恰好颜色不同的概率（请用“画树状图”或“列表”等方法写出分析过程）；
（2）现再将n个白球放入布袋，搅匀后，使摸出1个球是白球的概率为
，求n的值．
（1）摸出1个球，记下颜色后放回，并搅匀，再摸出1个球，求两次摸出的球恰好颜色不同的概率（请用“画树状图”或“列表”等方法写出分析过程）；
（2）现再将n个白球放入布袋，搅匀后，使摸出1个球是白球的概率为
| 3 |
| 4 |
考点：列表法与树状图法
专题：计算题
分析：（1）列表得出所有等可能的情况数，找出两次摸出的球恰好颜色不同的情况，即可求出所求的概率；
（2）根据题意列出关于n的方程，求出方程的解即可得到n的值．
（2）根据题意列出关于n的方程，求出方程的解即可得到n的值．
解答：解：（1）画树状图：
∴共有9种等可能的结果，其中符合条件的有4种情况，
∴P（两次摸到球颜色不同）=
；
（2）由题意得
=
，
解得：n=5，
经检验，n=5是所列方程的根，且符合题意．
| 红 | 红 | 白 | |
| 红 | （红，红） | （红，红） | （白，红） |
| 红 | （红，红） | （红，红） | （白，红） |
| 白 | （红，白） | （红，白） | （白，白） |
∴P（两次摸到球颜色不同）=
| 4 |
| 9 |
（2）由题意得
| 1+n |
| 3+n |
| 3 |
| 4 |
解得：n=5，
经检验，n=5是所列方程的根，且符合题意．
点评：此题考查了列表法与树状图法，用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
活力课时同步练习册系列答案
学业测评一课一测系列答案
相关题目
在平行四边形ABCD中，AB=6，AD=9，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE于点G，
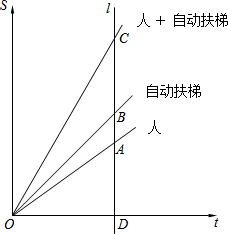如图，直线l与x轴垂直，垂足为D，它与从原点出发的三条射线分别交于点A、B、C．射线OA、OB、OC分别表示正常行走的人，站在自动扶梯上不走的人，在自动扶梯上同时正常行走的人所移动的路程s（m）与时间t（min）的函数关系，在这些关系中，正常行走的人的速度相同，自动扶梯的速度也相同．