题目内容
17．
如图所示，已知∠1=∠2，∠3=∠4，∠C=32°，∠D=28°，则∠P的度数为30°．
分析 利用“三角形的外角等于与它不相邻的两个内角和”列式子求解即可．
解答 
解：设AP与BC交于K，
∵在△ACK与△BPK中，∠AKC=∠PKB（对顶角相等），
∴∠P+∠3=∠1+∠C，即∠P=∠1-∠3+∠C，①
设AD与BP交于F，
同理有∠P=∠4-∠2+∠D，②
∵∠1=∠2，∠3=∠4，
∴①+②得，2∠P=∠C+∠D=32°+28°=60°，
∴∠P=30°．
故答案是：30°．
点评 本题考查的是三角形内角和定理及三角形外角的性质，熟知三角形的内角和外角之间的关系．三角形的外角等于与它不相邻的两个内角和是解答此题的关键．
练习册系列答案
相关题目
2．
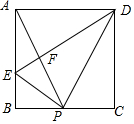如图，在矩形ABCD中，P是BC上一点，E是AB上一点，PD平分∠APC，PE⊥PD，连接DE交AP于F，在以下判断中，不正确的是（ ）
如图，在矩形ABCD中，P是BC上一点，E是AB上一点，PD平分∠APC，PE⊥PD，连接DE交AP于F，在以下判断中，不正确的是（ ）| A． | 当P为BC中点，△APD是等边三角形 | B． | 当△ADE∽△BPE时，P为BC中点 | ||
| C． | 当AE=2BE时，AP⊥DE | D． | 当△APD是等边三角形时，BE+CD=DE |
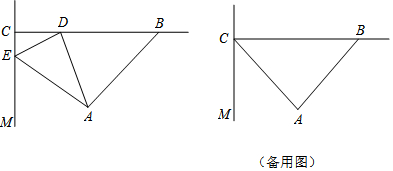
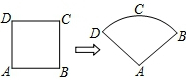如图，某数学兴趣小组将边长为6的正方形铁丝框ABCD变形为以A为圆心，AB为半径的扇形，则扇形的圆心角∠DAB的度数是$\frac{360}{π}$度．（结果保留π）
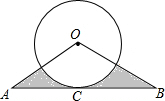如图，在△ABC中，OA=OB=6，∠O=120°，以点O为圆心的⊙O和底边AB相切于点C，则阴影部分的面积为9$\sqrt{3}$-3π．．