Question

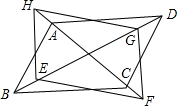如图，在?ABCD的对角线BD上取两点E，G，使BE=DG，在对角线AC的延长线上取两点F，H，使AH=CF，求证：四边形EFGH是平行四边形．

Answer 1

考点：平行四边形的判定与性质

专题：证明题

分析：设AC、BD相交于点O，则可得到OB=OD，OA=OC，结合条件可得到OE=OG、OH=OF，可证明四边形EFGH是平行四边形．

解答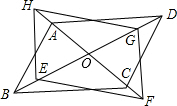：证明：设AC、BD相交于点O，
∵四边形ABCD为平行四边形，
∴OA=OC，OB=OD，
∵BE=DG，AH=CF，
∴OB-BE=OD-DG，OA+AH=OC+CF，
即OE=OG，OH=OF，
∴四边形EFGH是平行四边形．

点评：本题主要考查平行四边形的判定和性质，掌握平行四边形的判定和性质是解题的关键，即①两组对边分别平行的四边形?平行四边形，②两组对边分别相等的四边形?平行四边形，③一组对边平行且相等的四边形?平行四边形，④两组对角分别相等的四边形?平行四边形，⑤对角线互相平分的四边形?平行四边形．