题目内容
16. 小东从甲地出发匀速前往相距20km的乙地,一段时间后,小明从乙地出发沿同一条路匀速前往甲地.小东出发2.5h后,在距乙地7.5km处与小明相遇,之后两人同时到达终点.图中线段AB、CD分别表示小东、小明与乙地的距离y(km)与小东所用时间x(h)的关系.
小东从甲地出发匀速前往相距20km的乙地,一段时间后,小明从乙地出发沿同一条路匀速前往甲地.小东出发2.5h后,在距乙地7.5km处与小明相遇,之后两人同时到达终点.图中线段AB、CD分别表示小东、小明与乙地的距离y(km)与小东所用时间x(h)的关系.(1)求线段AB、CD所表示的y与x之间的函数表达式;
(2)小东出发多长时间后,两人相距16km?
分析 (1)分别利用A,B和(2.5,7.5),D点坐标求出函数解析式得出答案;
(2)利用①当0≤x<1.6时,②当1.6≤x<2.5时,y1-y2=16,③当2.5≤x≤4时,分别得出x的值进而得出答案.
解答 解:(1)设线段AB所表示的y与x之间的函数表达式为y1=kx+b,
由图象可知,函数图象经过点(0,20)、(2.5,7.5).
得$\left\{\begin{array}{l}{b=20}\\{2.5k+b=7.5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-5}\\{b=20}\end{array}\right.$,
所以线段AB所表示的y与x之间的函数表达式为y1=-5x+20.
令y1=0,得x=4.
所以B点的坐标为(4,0).所以D点的坐标为(4,20).
设线段CD所表示的y与x之间的函数表达式为y2=mx+n,
因为函数图象经过点(4,20)、(2.5,7.5).
得$\left\{\begin{array}{l}{4m+n=20}\\{2.5m+n=7.5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=\frac{25}{3}}\\{n=-\frac{40}{3}}\end{array}\right.$,
所以线段CD所表示的y与x之间的函数表达式为:y2=$\frac{25}{3}$x-$\frac{40}{3}$;
(2)线段CD所表示的y与x之间的函数表达式为y2=$\frac{25}{3}$x-$\frac{40}{3}$,
令y2=0,得x=1.6.即小东出发1.6 h后,小明开始出发.
①当0≤x<1.6时,y1=16,即-5x+20=16,
解得:x=0.8,
②当1.6≤x<2.5时,y1-y2=16,即-5x+20-($\frac{25}{3}$x-$\frac{40}{3}$)=16,
解得:x=1.3(舍去)
③当2.5≤x≤4时,y2-y1=16,即$\frac{25}{3}$x-$\frac{40}{3}$-(-5x+20)=16,
解得:x=3.7.
答:小东出发0.8h或3.7h后,两人相距16km.
点评 本题考查了一次函数的应用以及待定系数求一次函数解析式,解决本题的关键是利用分类讨论法得出x的值.

| A. | x2-x-2=(x-1)(x+2) | B. | -a2+a-$\frac{1}{4}$=$-\frac{1}{4}(2a-1)^{2}$ | ||
| C. | a(x-y)-b(y-x)=(x-y)(a-b) | D. | x2-4+2x=(x+2)(x-2)+2x |
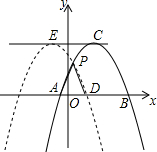 如图,抛物线y=-$\frac{4}{9}$(x-2)2+4交x轴于点A、B(点A在点B的左侧),其顶点为C,将抛物线沿x轴向左平移m(m>0)个单位,点B、C平移后的对应点为D、E,且两抛物线在x轴的上方交于点P,连接PA、PD.
如图,抛物线y=-$\frac{4}{9}$(x-2)2+4交x轴于点A、B(点A在点B的左侧),其顶点为C,将抛物线沿x轴向左平移m(m>0)个单位,点B、C平移后的对应点为D、E,且两抛物线在x轴的上方交于点P,连接PA、PD.