题目内容
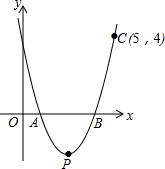 如图,抛物线y=ax2-5x+4a与x轴交于点A,B,且过点C(5,4).
如图,抛物线y=ax2-5x+4a与x轴交于点A,B,且过点C(5,4).(1)求a的值和该抛物线顶点P的坐标;
(2)若将该抛物线先向左平移3个单位,再向上平移4个单位,求出平移后抛物线的解析式.
考点:二次函数图象与几何变换,二次函数的性质
专题:
分析:(1)把点C代入函数关系式来求a的值;然后把该函数关系式利用配方法转化为顶点式方程,根据顶点式方程直接写出顶点P的坐标;
(2)根据“左加右减”的规律写出平移后的解析式.
(2)根据“左加右减”的规律写出平移后的解析式.
解答:解:(1)把C(5,4)代入y=ax2-5x+4a,得
25a-25+4a=4,
解得 a=1,
则该抛物线的函数关系式为:y=x2-5x+4=(x-
)2-
,即y=(x-
)2-
,
则P(
,
);
(2))∵抛物线原顶点坐标为(
,
),
∴平移后的顶点为(-
,-
),
∴平移后抛物线解析为:y═(x+
)2-
.
25a-25+4a=4,
解得 a=1,
则该抛物线的函数关系式为:y=x2-5x+4=(x-
| 5 |
| 2 |
| 9 |
| 4 |
| 5 |
| 2 |
| 9 |
| 4 |
则P(
| 5 |
| 2 |
| 9 |
| 4 |
(2))∵抛物线原顶点坐标为(
| 5 |
| 2 |
| 9 |
| 4 |
∴平移后的顶点为(-
| 3 |
| 2 |
| 1 |
| 4 |
∴平移后抛物线解析为:y═(x+
| 3 |
| 2 |
| 1 |
| 4 |
点评:主要考查的是二次函数图象与几何变换,由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
比x的相反数小2的数是( )
| A、-x+2 | B、-x-2 |
| C、-(x-2) | D、x-2 |
 如图,过P(1,1)和O点两点的圆交坐标轴于E、F两点,圆O1为△OEF的内切圆,切EF于M点,求OE-OF的值.
如图,过P(1,1)和O点两点的圆交坐标轴于E、F两点,圆O1为△OEF的内切圆,切EF于M点,求OE-OF的值. 将抛物线
将抛物线 如图所示,已知∠C=90°,AB⊥AC,D、E、B在一直线上,∠ADE=2∠EDC,求证:BE=2AD.
如图所示,已知∠C=90°,AB⊥AC,D、E、B在一直线上,∠ADE=2∠EDC,求证:BE=2AD. 如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG.试猜想线段AD与AG的关系,并证明你的猜想.
如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG.试猜想线段AD与AG的关系,并证明你的猜想.