题目内容
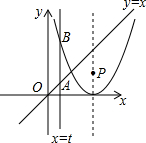 将抛物线y1=x2向右平移2个单位,得到抛物线y2的图象.P是抛物线y2对称轴上的一个动点,直线x=t平行于y轴,分别与直线y=x、抛物线y2交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则t=
将抛物线y1=x2向右平移2个单位,得到抛物线y2的图象.P是抛物线y2对称轴上的一个动点,直线x=t平行于y轴,分别与直线y=x、抛物线y2交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则t=考点:二次函数图象与几何变换
专题:
分析:根据向右平移,横坐标减表示出抛物线y2的函数解析式,然后表示出点A、B的坐标,再表示出AB的长度与AP的长度,然后根据等腰直角三角形的两直角边相等列出方程求解即可.
解答:解:∵抛物线y1=x2向右平移2个单位,
∴抛物线y2的函数解析式为y=(x-2)2=x2-4x+4,
∴抛物线y2的对称轴为直线x=2,
∵直线x=t与直线y=x、抛物线y2交于点A、B,
∴点A的坐标为(t,t),点B的坐标为(t,t2-4t+4),
∴AB=|t2-4t+4-t|=|t2-5t+4|,
AP=|t-2|,
∵△APB是以点A或B为直角顶点的三角形,
∴|t2-5t+4|=|t-2|,
∴t2-5t+4=t-2①或t2-5t+4=-(t-2)②,
整理①得,t2-6t+6=0,
解得t1=3+
,t2=3-
,
整理②得,t2-4t+2=0,
解得t1=2+
,t2=2-
,
综上所述,满足条件的t值为:3+
或3-
或2+
或2-
,
故答案为:3+
或3-
或2+
或2-
.
∴抛物线y2的函数解析式为y=(x-2)2=x2-4x+4,
∴抛物线y2的对称轴为直线x=2,
∵直线x=t与直线y=x、抛物线y2交于点A、B,
∴点A的坐标为(t,t),点B的坐标为(t,t2-4t+4),
∴AB=|t2-4t+4-t|=|t2-5t+4|,
AP=|t-2|,
∵△APB是以点A或B为直角顶点的三角形,
∴|t2-5t+4|=|t-2|,
∴t2-5t+4=t-2①或t2-5t+4=-(t-2)②,
整理①得,t2-6t+6=0,
解得t1=3+
| 3 |
| 3 |
整理②得,t2-4t+2=0,
解得t1=2+
| 2 |
| 2 |
综上所述,满足条件的t值为:3+
| 3 |
| 3 |
| 2 |
| 2 |
故答案为:3+
| 3 |
| 3 |
| 2 |
| 2 |
点评:本题考查了二次函数图象与几何变换,等腰直角三角形的性质,根据抛物线与直线的解析式表示出AB、AP或(BP)的长,然后根据等腰直角三角形的性质列出方程是解题的关键.

练习册系列答案
相关题目
若实数m满足(m2-m+1)(m2-m+1)=4,则m2-m的值为( )
| A、1或-3 | B、1 | C、-3 | D、0 |
 如图,AB是⊙O的直径,AB=18,点C、D在⊙O上,且AC=CD=6,求弦BD的长.
如图,AB是⊙O的直径,AB=18,点C、D在⊙O上,且AC=CD=6,求弦BD的长.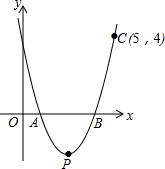 如图,抛物线y=ax2-5x+4a与x轴交于点A,B,且过点C(5,4).
如图,抛物线y=ax2-5x+4a与x轴交于点A,B,且过点C(5,4).