题目内容
 如图,过P(1,1)和O点两点的圆交坐标轴于E、F两点,圆O1为△OEF的内切圆,切EF于M点,求OE-OF的值.
如图,过P(1,1)和O点两点的圆交坐标轴于E、F两点,圆O1为△OEF的内切圆,切EF于M点,求OE-OF的值.考点:圆的综合题
专题:计算题
分析:设E(a,0),F(0,b),根据圆周角定理由∠EOF=90°可判断EF为△OEF为外接圆的直径,利用线段中点坐标公式得到EF的中点T的坐标为(
,
),根据半径相等和两点间的距离公式得到(
)2+(
)2=(
-1)2+(
-1)2,整理得到a+b=2,于是可得OE-OF=2.
| a |
| 2 |
| b |
| 2 |
| a |
| 2 |
| b |
| 2 |
| a |
| 2 |
| b |
| 2 |
解答:解:设E(a,0),F(0,b),
∵∠EOF=90°,
∴EF为△OEF为外接圆的直径,
即EF的中点T为△OEF为外接圆的圆心,
∴T的坐标为(
,
),
∵TO=TP,
∴(
)2+(
)2=(
-1)2+(
-1)2,
∴a+b=2,
∵OE=a,OF=-b,
∴OE-OF=a-(-b)=a+b=2.
∵∠EOF=90°,
∴EF为△OEF为外接圆的直径,
即EF的中点T为△OEF为外接圆的圆心,
∴T的坐标为(
| a |
| 2 |
| b |
| 2 |
∵TO=TP,
∴(
| a |
| 2 |
| b |
| 2 |
| a |
| 2 |
| b |
| 2 |
∴a+b=2,
∵OE=a,OF=-b,
∴OE-OF=a-(-b)=a+b=2.
点评:本题考查了圆的综合题:熟练掌握圆周角定理;会利用两点间的距离公式计线段的长;理解坐标与图形性质.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
若实数m满足(m2-m+1)(m2-m+1)=4,则m2-m的值为( )
| A、1或-3 | B、1 | C、-3 | D、0 |
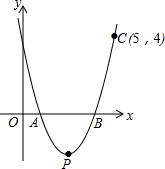 如图,抛物线y=ax2-5x+4a与x轴交于点A,B,且过点C(5,4).
如图,抛物线y=ax2-5x+4a与x轴交于点A,B,且过点C(5,4).