题目内容
如图，由∠1=∠2，∠D=∠B，推出以下结论，其中错误的是（ ）| A、AB∥DC |
| B、AD∥BC |
| C、∠DAB=∠BCD |
| D、∠DCA=∠DAC |
考点：平行线的判定与性质
专题：
分析：根据内错角相等，两直线平行可得AB∥DC，再根据两直线平行，同旁内角互补可得∠D+∠BAD=180°，∠B+∠BCD=90°然后求出∠B+∠BAD=180°，再根据同旁内角互补，两直线平行可得AD∥BC，根据等角的补角相等可得∠DAB=∠BCD；∠DCA=∠DAC无法求出．
解答：解：∵∠1=∠2，
∴AB∥DC，故A选项结论正确；
∴∠D+∠BAD=180°，∠B+∠BCD=90°，
∵∠D=∠B，
∴∠B+∠BAD=180°，∠DAB=∠BCD，故C选项结论正确；
∴AD∥BC，故B选项结论正确；
只有AC平分∠BAD时，∠DCA=∠DAC，故D选项结论错误．
故选D．
∴AB∥DC，故A选项结论正确；
∴∠D+∠BAD=180°，∠B+∠BCD=90°，
∵∠D=∠B，
∴∠B+∠BAD=180°，∠DAB=∠BCD，故C选项结论正确；
∴AD∥BC，故B选项结论正确；
只有AC平分∠BAD时，∠DCA=∠DAC，故D选项结论错误．
故选D．
点评：本题考查了平行线的判定与性质，熟记性质并准确识图理清图中各角度之间的关系是解题的关键．
练习册系列答案
相关题目
小兰家的窗户装饰物如图，它是由四个半圆组成（半径分别相同），窗户能射进阳光部分的面积是
如图，△ABC的三个顶点均在方格纸的格点上，B、C两点的位置分别用有序数对（0，-2）、（3，-1）表示，将△ABC平移后，点C的对应点C1的位置为（1，2），则点A的对应点A1的位置为（ ）| A、（-1，2） |
| B、（-1，3） |
| C、（-2，1） |
| D、（-2，3） |
若方程3m（x+1）+1=m（3-x）-5x的解是正数，则m的取值范围是（ ）
A、m＞
| ||
B、m＜
| ||
C、m＞-
| ||
D、m＜-
|
若（y+3）（y-2）=y2+my+n，则（3m+n）-2的值是（ ）
| A、6 | ||
| B、9 | ||
C、
| ||
D、
|
下列说法正确的是（ ）
| A、a的系数是0 | ||
B、
| ||
| C、0是单项式 | ||
| D、-5y的系数是5 |
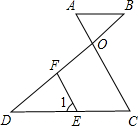已知：如图，AB∥DC，AC和BD相交于点O，E是CD上一点，F是OD上一点，且∠1=∠A．