题目内容
关于x的函数y=（m2-1）x2-（2m+2）x+2的图象与x轴只有一个公共点，求m的值．
考点：抛物线与x轴的交点,一次函数图象上点的坐标特征
专题：计算题
分析：需要分类讨论：该函数是一次函数和二次函数两种情况．
解答：解：①当m2-1=0，且2m+2≠0，即m=1时，该函数是一次函数，则其图象与x轴只有一个公共点；
②当m2-1≠0，即m≠±1时，该函数是二次函数，则
△=（2m+2）2-8（m2-1）=0，
解得 m=3，m=-1（舍去）．
综上所述，m的值是1或3．
②当m2-1≠0，即m≠±1时，该函数是二次函数，则
△=（2m+2）2-8（m2-1）=0，
解得 m=3，m=-1（舍去）．
综上所述，m的值是1或3．
点评：本题考查了抛物线与x轴的交点．注意一定要分类讨论，以防漏解．
练习册系列答案
相关题目
如图，△ABC的三个顶点均在方格纸的格点上，B、C两点的位置分别用有序数对（0，-2）、（3，-1）表示，将△ABC平移后，点C的对应点C1的位置为（1，2），则点A的对应点A1的位置为（ ）| A、（-1，2） |
| B、（-1，3） |
| C、（-2，1） |
| D、（-2，3） |
下列运算不正确的是（ ）
| A、（a2）3=a6 |
| B、a2-a3=a5 |
| C、a3÷a2=a |
| D、a2•a3=a5 |
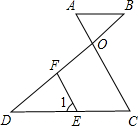已知：如图，AB∥DC，AC和BD相交于点O，E是CD上一点，F是OD上一点，且∠1=∠A．
如图，方格纸中的每个小方格都是边长为1个单位的正方形，△ABC的顶点均在格点上，直线a为对称轴，A和C都在对称轴上．