题目内容
10.已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=9cm.如图(2),△DEF从图(1)的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿BA向点A匀速移动,当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由;
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.

分析 (1)利用垂直平分线的性质可得AP=AQ,易得∠EQC=45°,可得CE=CQ,由CE=t,则BP=2t,CQ=t,∴AQ=8-t,利用勾股定理可得AB,则AP=10-2t,AQ=8-t,可得10-2t=8-t,解得t;
(2)过P作PM⊥BE,交BE于M,由$sinB=\frac{AC}{AB}=\frac{PM}{BP}$可得PM,因为y=S△ABC-S△BPE,易得y与t的函数关系式,利用二次函数的最值可得y的最小值;
(3)假设存在某一时刻t,使点P、Q、F三点在同一条直线上,过P作PN⊥AC,交AC于N,易得△PAN∽△BAC,利用相似三角形的性质可得PN,AN,NQ,因为∠ACB=90°,B、C(E)、F在同一条直线上,可得△QCF∽△QNP,利用相似三角形的性质列式,可解得结果.
解答 解:(1)如图(1),∵点A在线段PQ的垂直平分线上,∴AP=AQ,
∵∠DEF=45°,∠ACB=90°,∠DEF+∠ACB+∠EQC=180°,
∴∠EQC=45°,∴∠DEF=∠EQC,∴CE=CQ,
由题意知:CE=t,BP=2t,
∴CQ=t,∴AQ=8-t,
在Rt△ABC中,由勾股定理得:AB=10cm,
则AP=10-2t,∴10-2t=8-t,
解得:t=2,
答:当t=2s时,点A在线段PQ的垂直平分线上;
(2)如图(2),过P作PM⊥BE,交BE于M,
∴∠BMP=90°,
在Rt△ABC和Rt△BPM中,
∴$sinB=\frac{AC}{AB}=\frac{PM}{BP}$,∴$\frac{PM}{2t}=\frac{10}{8}$,
∴PM=$\frac{8}{5}t$,
∵BC=6cm,CE=t,∴BE=6-t,
∴y=S△ABC-S△BPE
=$\frac{1}{2}BC•AC-\frac{1}{2}BE•PM=\frac{1}{2}×6×8-\frac{1}{2}×(6-t)×\frac{8}{5}t$
=$\frac{4}{5}{t^2}-\frac{24}{5}t+24=\frac{4}{5}{(t-3)^2}+\frac{84}{5}$,
∵$a=\frac{4}{5}>0$,
∴抛物线开口向上,
∴当t=3时,y最小=$\frac{84}{5}$,
答:当t=3s时,四边形APEC的面积最小,最小面积为 $\frac{84}{5}$cm2;
(3)如图(3),假设存在某一时刻t,使点P、Q、F三点在同一条直线上,
过P作PN⊥AC,交AC于N,
∴∠ANP=∠ACB=∠PNQ=90°,
∵∠PAN=∠BAC,∴△PAN∽△BAC,
∴$\frac{PN}{BC}=\frac{AP}{AB}=\frac{AN}{AC}$,∴$\frac{PN}{6}=\frac{10-2t}{10}=\frac{AN}{8}$,∴$PN=6-\frac{6}{5}t$,$AN=8-\frac{8}{5}t$,
∵NQ=AQ-AN,
∴NQ=$8-t-(8-\frac{8}{5}t)=\frac{3}{5}t$,
∵∠ACB=90°,B、C(E)、F在同一条直线上,
∴∠QCF=90°,∠QCF=∠PNQ,
∵∠FQC=∠PQN,∴△QCF∽△QNP,
∴$\frac{PN}{FC}=\frac{NQ}{CQ}$,∴$\frac{{6-\frac{6}{5}t}}{9-t}=\frac{{\frac{3}{5}t}}{t}$,
∵0<t<4.5,
∴$\frac{{6-\frac{6}{5}t}}{9-t}=\frac{3}{5}$,
解得:t=1,
答:当t=1s,点P、Q、F三点在同一条直线上.
点评 本题主要考查了相似三角形的性质及判定,作恰当的辅助线,构建直角三角形是解答此题的关键.

| A. | 对角线互相平分的四边形是平行四边形 | |
| B. | 两组对边分别相等的四边形是平行四边形 | |
| C. | 一组对边平行且相等的四边形是平行四边形 | |
| D. | 一组对边相等,另一组对边平行的四边形是平行四边形 |
 小宇在学习解直角三角形的知识后,萌生了测量他家对面位于同一水平面的楼房高度的想法,他站在自家C处测得对面楼房底端B的俯角为45°,测得对面楼房顶端A的仰角为30°,并量得两栋楼房间的距离为9米,请你用小宇测得的数据求出对面楼房AB的高度.(结果保留到整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
小宇在学习解直角三角形的知识后,萌生了测量他家对面位于同一水平面的楼房高度的想法,他站在自家C处测得对面楼房底端B的俯角为45°,测得对面楼房顶端A的仰角为30°,并量得两栋楼房间的距离为9米,请你用小宇测得的数据求出对面楼房AB的高度.(结果保留到整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)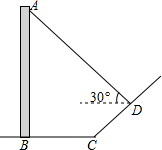 如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)
如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号) 如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:①∠ADG=22.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG;⑥若S△OGF=1,则正方形ABCD的面积是6+4$\sqrt{2}$,其中正确的结论个数为( )
如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:①∠ADG=22.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG;⑥若S△OGF=1,则正方形ABCD的面积是6+4$\sqrt{2}$,其中正确的结论个数为( )