题目内容
12.一个口袋中有16个白球和若干个黑球,在不允许将球倒出来的前提下,为估计口袋中黑球的个数,采用了如下的方法:从口袋中摸出1个球记下颜色放回摇匀,不断重复上述过程多次,发现摸到黑球的频率稳定在0.8,根据上述数据,可估计口袋中大约有64个黑球.分析 根据口袋中有16个白球和x个黑球,利用摸到黑球的频率稳定在0.8列出方程,求解即可.
解答 解:设口袋中有16个白球和x个黑球,
根据题意,得$\frac{x}{16+x}$=0.8,
解得x=64.
经检验,x=64是原方程的解.
估计口袋中大约有64个黑球.
故答案为:64.
点评 此题主要考查了利用频率估计概率,大量反复试验下频率稳定值即概率.关键是根据黑球的频率得到相应的等量关系.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
2.下列各式计算正确的是( )
| A. | $8\sqrt{3}-2\sqrt{3}=6$ | B. | $5\sqrt{3}+5\sqrt{2}=10\sqrt{5}$ | C. | $4\sqrt{3}×2\sqrt{2}=8\sqrt{6}$ | D. | $4\sqrt{2}÷2\sqrt{2}=2\sqrt{2}$ |
3.下列运算正确的是( )
| A. | x6•x2=x12 | B. | x2+x2=2x2 | C. | (x2)3=x5 | D. | x6÷x2=x3 |
20. 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=4,H是AF的中点,那么CH的长是( )
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=4,H是AF的中点,那么CH的长是( )
 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=4,H是AF的中点,那么CH的长是( )
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=4,H是AF的中点,那么CH的长是( )| A. | $\sqrt{10}$ | B. | $\sqrt{5}$ | C. | $\frac{3}{2}\sqrt{2}$ | D. | 2 |
7.下列关于比例线段和相似的叙述,不正确的是( )
| A. | 若a:b=c:d,则ac=bd | |
| B. | 相似三角形的面积比等于相似比的平方 | |
| C. | 点C是线段AB的黄金分割点,且AC>BC,则$\frac{BC}{AB}=\frac{{3-\sqrt{5}}}{2}$ | |
| D. | 经过位似多边形对应顶点的直线一定交于同一点 |
1.若x的相反数是$\frac{1}{3}$,那么x的倒数是( )
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | $-\frac{1}{3}$ |
2. 如图所示,上午8时,一艘船从A处出发,以15海里/时的速度向正北方向航行,11时到达B处,分别从A、B处望灯塔C,测得∠NAC=36°,∠NBC=72°,则从B处到灯塔C的距离是( )
如图所示,上午8时,一艘船从A处出发,以15海里/时的速度向正北方向航行,11时到达B处,分别从A、B处望灯塔C,测得∠NAC=36°,∠NBC=72°,则从B处到灯塔C的距离是( )
 如图所示,上午8时,一艘船从A处出发,以15海里/时的速度向正北方向航行,11时到达B处,分别从A、B处望灯塔C,测得∠NAC=36°,∠NBC=72°,则从B处到灯塔C的距离是( )
如图所示,上午8时,一艘船从A处出发,以15海里/时的速度向正北方向航行,11时到达B处,分别从A、B处望灯塔C,测得∠NAC=36°,∠NBC=72°,则从B处到灯塔C的距离是( )| A. | 15海里 | B. | 10海里 | C. | 30海里 | D. | 45海里 |
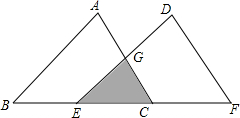 如图,将△ABC沿AB方向平移得到△DEF,△ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC的$\frac{1}{3}$.已知BC=3,求△ABC平移的距离.
如图,将△ABC沿AB方向平移得到△DEF,△ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC的$\frac{1}{3}$.已知BC=3,求△ABC平移的距离.