题目内容
6.已知二次函数y=ax2+bx-1(a≠0)的图象经过点(1,1),则代数式1-a-b的值为( )| A. | -1 | B. | 2 | C. | -3 | D. | 5 |
分析 把点(1,1)代入函数解析式求出a+b-1,然后即可得解.
解答 解:∵二次函数y=ax2+bx-1(a≠0)的图象经过点(1,1),
∴a+b-1=1,
∴1-a-b=-1.
故选A.
点评 本题考查了二次函数图象上点的坐标特征,整体思想的利用是解题的关键.

练习册系列答案
相关题目
17.下列函数中,是反比例函数的是( )
| A. | y=$\frac{k}{x}$ | B. | 3x+2y=0 | C. | xy-$\sqrt{2}$=0 | D. | y=$\frac{2}{x+1}$ |
14.已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
则下列判断正确的是( )
| x | … | -1 | 0 | 1 | 3 | … |
| y | … | -3 | 1 | 3 | 1 | … |
| A. | 抛物线开口向上 | B. | 抛物线与y轴交于负半轴 | ||
| C. | 当x=4时,y>0 | D. | 方程ax2+bx+c=0的正根在3与4之间 |
1. 如图所示的图案绕旋转中心旋转一定角度后能够与自身重合,那么这个旋转角可能是( )
如图所示的图案绕旋转中心旋转一定角度后能够与自身重合,那么这个旋转角可能是( )
 如图所示的图案绕旋转中心旋转一定角度后能够与自身重合,那么这个旋转角可能是( )
如图所示的图案绕旋转中心旋转一定角度后能够与自身重合,那么这个旋转角可能是( )| A. | 60° | B. | 72° | C. | 90° | D. | 120° |
11.已知-2与m互为相反数,则m的值是( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
18.下列交通标志图形好是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
15.下列平面图形中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16.下列性质中,菱形具有矩形不一定具有的是( )
| A. | 对角线相等 | B. | 对角线互相平分 | C. | 邻边互相垂直 | D. | 对角线互相垂直 |
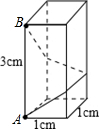 如图,长方体的底面是边长为1cm 的正方形,高为3cm.
如图,长方体的底面是边长为1cm 的正方形,高为3cm.