题目内容
14.如果点P(6-2x,x-1)在第四象限,那么x的取值范围是( )| A. | x>3 | B. | x<3 | C. | x>1 | D. | x<1 |
分析 根据点的坐标在象限内的特点得出不等式组,求出不等式组的解集即可.
解答 解:∵点P(6-2x,x-1)在第四象限,
∴$\left\{\begin{array}{l}{6-2x>0}\\{x-1<0}\end{array}\right.$,
解不等式组得:x<1,
故选D.
点评 本题考查了解一元一次不等式组,点的坐标的应用,能根据点的坐标特点得出不等式组是解此题的关键.

练习册系列答案
相关题目
6.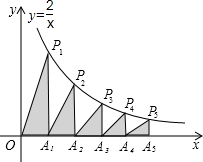 如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5,并设其面积分别为S1、S2、S3、S4、S5,则S5的值为( )
如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5,并设其面积分别为S1、S2、S3、S4、S5,则S5的值为( )
 如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5,并设其面积分别为S1、S2、S3、S4、S5,则S5的值为( )
如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5,并设其面积分别为S1、S2、S3、S4、S5,则S5的值为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{5}$ |




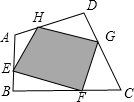 如图,四边形ABCD中,E,F,G,H分别是边AB、BC、CD、DA上的点,且AH=$\frac{1}{3}$AD,BE=$\frac{1}{3}$AB,CF=$\frac{1}{3}$BC,DG=$\frac{1}{3}$CD,如果阴影部分的面积为10平方厘米,则四边形ABCD的面积等于18平方厘米.
如图,四边形ABCD中,E,F,G,H分别是边AB、BC、CD、DA上的点,且AH=$\frac{1}{3}$AD,BE=$\frac{1}{3}$AB,CF=$\frac{1}{3}$BC,DG=$\frac{1}{3}$CD,如果阴影部分的面积为10平方厘米,则四边形ABCD的面积等于18平方厘米. 在菱形ABCD中,E为AB的中点,OE=5,则菱形ABCD的边长为10.
在菱形ABCD中,E为AB的中点,OE=5,则菱形ABCD的边长为10.