题目内容
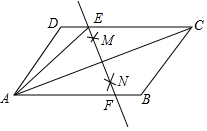
7.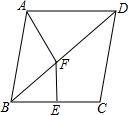 如图,在菱形ABCD中,∠ABC=40°,BC的垂直平分线EF交对角线BD于点F.连接AF,则∠DAF的度数为120°.
如图,在菱形ABCD中,∠ABC=40°,BC的垂直平分线EF交对角线BD于点F.连接AF,则∠DAF的度数为120°.
分析 连接FC,根据菱形是轴对称图形可得∠DAF=∠CFD,再根据菱形的性质可得AB∥CD,∠DBC=$\frac{1}{2}$∠ABC,进而可得∠BCD和∠FBC的度数,然后根据线段垂直平分线的性质可得∠FCB的度数,进而可得∠FCD的度数,从而可得答案.
解答 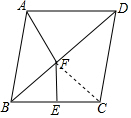 解:连接FC,
解:连接FC,
∵四边形ABCD是菱形,
∴四边形ABCD是轴对称图形,
∴∠DAF=∠CFD,
∵四边形ABCD是菱形,
∴AB∥CD,∠DBC=$\frac{1}{2}$∠ABC,
∵∠ABC=40°,
∴∠BCD=140°,∠FBC=20°,
∵EF是BC的垂直平分线,
∴FB=FC,
∴∠FBC=∠FCB=20°,
∴∠FCD=120°,
∴∠DAF=120°,
故答案为:120°.
点评 此题主要考查了菱形的性质,以及线段垂直平分线的性质,关键是掌握菱形是轴对称图形,菱形两条对角线互相垂直,并且每一条对角线平分一组对角.

练习册系列答案
相关题目
18.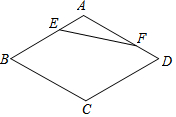 如图,在菱形ABCD中,∠B=60°,AB=a,点E,F分别是边AB,AD上的动点,且AE+AF=a,则线段EF的最小值为( )
如图,在菱形ABCD中,∠B=60°,AB=a,点E,F分别是边AB,AD上的动点,且AE+AF=a,则线段EF的最小值为( )
 如图,在菱形ABCD中,∠B=60°,AB=a,点E,F分别是边AB,AD上的动点,且AE+AF=a,则线段EF的最小值为( )
如图,在菱形ABCD中,∠B=60°,AB=a,点E,F分别是边AB,AD上的动点,且AE+AF=a,则线段EF的最小值为( )| A. | 2$\sqrt{3}$a | B. | $\frac{\sqrt{3}}{2}$a | C. | $\sqrt{3}$a | D. | $\frac{a}{2}$ |
12.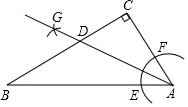 如图,在△ABC中,∠C=90°,AB=8,AC=4,以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E、F,再分别以点E、F为圆心,大于EF长为半径画弧,两弧交于点G,作射线AG,交BC于点D,则D到AB的距离为( )
如图,在△ABC中,∠C=90°,AB=8,AC=4,以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E、F,再分别以点E、F为圆心,大于EF长为半径画弧,两弧交于点G,作射线AG,交BC于点D,则D到AB的距离为( )
 如图,在△ABC中,∠C=90°,AB=8,AC=4,以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E、F,再分别以点E、F为圆心,大于EF长为半径画弧,两弧交于点G,作射线AG,交BC于点D,则D到AB的距离为( )
如图,在△ABC中,∠C=90°,AB=8,AC=4,以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E、F,再分别以点E、F为圆心,大于EF长为半径画弧,两弧交于点G,作射线AG,交BC于点D,则D到AB的距离为( )| A. | 2 | B. | 4 | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
 在平行四边形ABCD中,连接AC,按以下步骤作图,分别以A、C为圆心,以大于$\frac{1}{2}$AC的长为半径画弧,两弧分别相交于点M、N,作直线MN交CD于点E,交AB于点F.若AB=6,BC=4,则△ADE的周长为10.
在平行四边形ABCD中,连接AC,按以下步骤作图,分别以A、C为圆心,以大于$\frac{1}{2}$AC的长为半径画弧,两弧分别相交于点M、N,作直线MN交CD于点E,交AB于点F.若AB=6,BC=4,则△ADE的周长为10.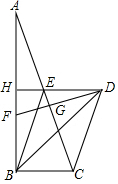 如图,在Rt△ABC中,∠ABC=90°,DH垂直平分AB交AC于点E,连接BE、CD,CD=CE,点F在AB上,BF=BC,连接BD,BD平分∠ABC.
如图,在Rt△ABC中,∠ABC=90°,DH垂直平分AB交AC于点E,连接BE、CD,CD=CE,点F在AB上,BF=BC,连接BD,BD平分∠ABC.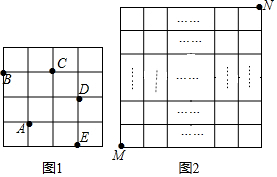
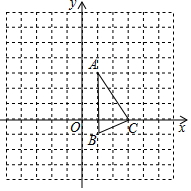 如图,△ABC位于直角坐标系内,且三个顶点均在正方形的网格的顶点上.
如图,△ABC位于直角坐标系内,且三个顶点均在正方形的网格的顶点上.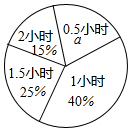 某校为了解学生每天参加户外活动的情况,随机抽查了100名学生每天参加户外活动的时间情况,并将抽查结果绘制成如图所示的扇形统计图.
某校为了解学生每天参加户外活动的情况,随机抽查了100名学生每天参加户外活动的时间情况,并将抽查结果绘制成如图所示的扇形统计图.