题目内容
4. 如图,在四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在直线BC,DC上分别找一点M,N,使得△AMN的周长最小时,则∠MAN的度数为60°.
如图,在四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在直线BC,DC上分别找一点M,N,使得△AMN的周长最小时,则∠MAN的度数为60°.
分析 根据要使△AMN的周长最小,即利用点的对称,让三角形的三边在同一直线上,作出A关于BC和CD的对称点A′,A″,即可得出∠AA′M+∠A″=∠HAA′=60°,进而得出∠AMN+∠ANM=2(∠AA′M+∠A″)即可得出答案.
解答 解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.作DA延长线AH,
∵∠DAB=120°,
∴∠HAA′=60°,
∴∠AA′M+∠A″=∠HAA′=60°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×60°=120°,
∴∠MAN=60°,
故答案为:60°.
点评 此题主要考查了平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出M,N的位置是解题关键.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
15.下列事件中,必然事件是( )
| A. | 任意掷一枚均匀的硬币,正面朝上 | |
| B. | 从一副扑克牌中,随意抽出一张是大王 | |
| C. | 通常情况下,抛出的篮球会下落 | |
| D. | 三角形内角和为360° |
19.在π,$\sqrt{3}$,1.732,3.14四个数中,无理数的个数是( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 没有 |
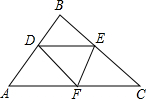 如图,在△ABC中,AB,BC,CA的长分别为6,7,8,且D,E,F分别是AB,BC,CA的中点,依次连接D,E,F得到△DEF,则△DEF的周长为10.5.
如图,在△ABC中,AB,BC,CA的长分别为6,7,8,且D,E,F分别是AB,BC,CA的中点,依次连接D,E,F得到△DEF,则△DEF的周长为10.5.