题目内容
16.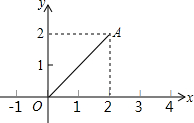 如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P的坐标不可能是( )
如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P的坐标不可能是( )| A. | (4,0) | B. | (-2$\sqrt{2}$,0) | C. | (1,0) | D. | (2,0) |
分析 先根据勾股定理求出OA的长,再根据①AP=PO;②AO=AP;③AO=OP分别算出P点坐标即可.
解答  解:点A的坐标是(2,2),
解:点A的坐标是(2,2),
根据勾股定理可得:OA=2$\sqrt{2}$,
①若AP=PO,可得:P(2,0),
②若AO=AP可得:P(4,0),
③若AO=OP,可得:P(2$\sqrt{2}$,0)或(-2$\sqrt{2}$,0),
∴P(2,0),(4,0),(-2$\sqrt{2}$,0),
故点P的坐标不可能是:(1,0).
故选C.
点评 此题主要考查了坐标与图形的性质,等腰三角形的判定,关键是掌握等腰三角形的判定:有两边相等的三角形是等腰三角形,再分情况讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列各数中,是最简二次根式的是( )
| A. | $\sqrt{\frac{1}{5}}$ | B. | $\sqrt{50}$ | C. | $\sqrt{7}$ | D. | $\sqrt{25}$ |
11.观察下列算式:
31=3,32=9,33=27,34=81,35=243,36=729,37=2187,38=6561,…根据上述算式中的规律,你认为32016的末位数字是( )
31=3,32=9,33=27,34=81,35=243,36=729,37=2187,38=6561,…根据上述算式中的规律,你认为32016的末位数字是( )
| A. | 1 | B. | 9 | C. | 7 | D. | 3 |
5.用一个平面去解一个正方体,截面性状不可能的是( )
| A. | 三角形 | B. | 长方体 | C. | 梯形 | D. | 圆 |

 若干个相同的小立方体搭成的几何体从上面和从左面看到的形状如图所示,则满足条件的几何体中小立方体的个数最少是5.
若干个相同的小立方体搭成的几何体从上面和从左面看到的形状如图所示,则满足条件的几何体中小立方体的个数最少是5. 如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,AE=3ED,如果AC=12cm,那么DE的长为3cm.
如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,AE=3ED,如果AC=12cm,那么DE的长为3cm. 已知:P是正方形ABCD对角线AC上一点,PE⊥AB,PF⊥BC,E、F分别为垂足,求证:DP=EF.
已知:P是正方形ABCD对角线AC上一点,PE⊥AB,PF⊥BC,E、F分别为垂足,求证:DP=EF.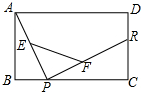 如图,矩形ABCD中,AD=13,DC=10,P是BC上的一点,R、E、F分别是DC、AP、RP的中点,当点P在BC上由B向C移动时,那么EF的长度$\frac{\sqrt{194}}{2}$.
如图,矩形ABCD中,AD=13,DC=10,P是BC上的一点,R、E、F分别是DC、AP、RP的中点,当点P在BC上由B向C移动时,那么EF的长度$\frac{\sqrt{194}}{2}$.