题目内容
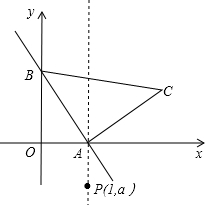 已知,直线y=-
已知,直线y=-| 3 |
| 3 |
(1)则三角形ABC的面积S△ABC=
(2)证明不论a取任何实数,△BOP的面积是一个常数;
(3)要使得△ABC和△ABP的面积相等,求实数a的值.
考点:一次函数综合题
专题:
分析:(1)先求出A、B两点的坐标,利用勾股定理得到AB的长,等腰Rt△ABC的面积为AB平方的一半;
(2)三角形BOP的底边BO=
,BO边上的高为P点的横坐标1,所以它的面积是一个常数
;
(3)实际上给定△ABP的面积,求P点坐标.利用面积和差求△ABP的面积,注意要分类讨论.
(2)三角形BOP的底边BO=
| 3 |
| ||
| 2 |
(3)实际上给定△ABP的面积,求P点坐标.利用面积和差求△ABP的面积,注意要分类讨论.
解答: 解:(1)令y=-
解:(1)令y=-
x+
中x=0,得点B坐标为(0,
);
令y=0,得点A坐标为(1,0).
由勾股定理可得AB=
=2,
所以S△ABC=
AB2=
×4=2;
作CD⊥x轴于点D,
∴△BAO≌△ACD,
∴DA=BO=
,CD=AO=1,
∴点C的坐标为(1+
,1);
(2)不论a取任何实数,△BOP都可以以BO=
为底,点P到y轴的距离1为高,
∴S△BOP=
为常数;
(3)当点P在第四象限时,
∵S△ABO=
,S△APO=-
a∴S△ABP=S△ABO+S△APO-S△BOP=S△ABC=2,
即
-
a-
=2解得a=-4,
(或S△ABP=-
即-
=2解得a=-4)
当点P在第一象限时,同理可得a=4
综上,a=±4
 解:(1)令y=-
解:(1)令y=-| 3 |
| 3 |
| 3 |
令y=0,得点A坐标为(1,0).
由勾股定理可得AB=
12+(
|
所以S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
作CD⊥x轴于点D,
∴△BAO≌△ACD,
∴DA=BO=
| 3 |
∴点C的坐标为(1+
| 3 |
(2)不论a取任何实数,△BOP都可以以BO=
| 3 |
∴S△BOP=
| ||
| 2 |
(3)当点P在第四象限时,
∵S△ABO=
| ||
| 2 |
| 1 |
| 2 |
即
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
(或S△ABP=-
| a |
| 2 |
| a |
| 2 |
当点P在第一象限时,同理可得a=4
综上,a=±4
点评:本题考查了一次函数的综合知识,掌握一次函数的性质,会求一次函数与两坐标轴的交点坐标;会用坐标表示线段;掌握用面积的和差表示不规则图形的面积.

练习册系列答案
相关题目
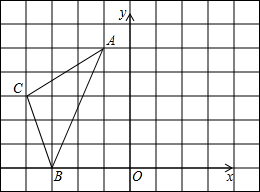 如图,在直角坐标系xOy中,A(-l,5),B(-3,0),C(-4,3).
如图,在直角坐标系xOy中,A(-l,5),B(-3,0),C(-4,3).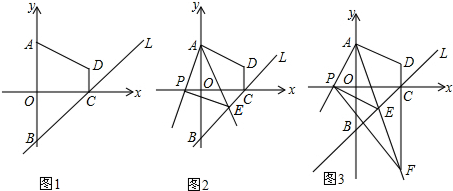
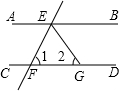 如图:AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2等于多少度?
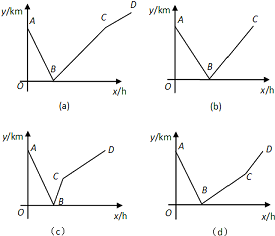
如图:AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2等于多少度?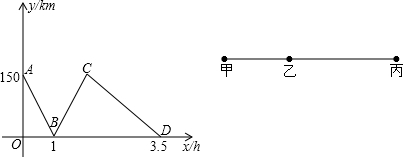 两车同时出发同向而行,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
两车同时出发同向而行,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究: