题目内容
16.问题情境:如图1,P是⊙O外的一点,直线PO分别交⊙O于点A、B,则PA是点P到⊙O上的点的最短距离.
探究:
请您结合图2给予证明,
归纳:
圆外一点到圆上各点的最短距离是:这点到连接这点与圆心连线与圆交点之间的距离.
图中有圆,直接运用:
如图3,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是$\widehat{CD}$上的一个动点,连接AP,则AP的最小值是$\sqrt{7}$-1.
图中无圆,构造运用:
如图4,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,请求出A′C长度的最小值.
解:由折叠知A′M=AM,又M是AD的中点,可得MA=MA'=MD,故点A'在以AD为直径的圆上.如图8,以点M为圆心,MA为半径画⊙M,过M作MH⊥CD,垂足为H,(请继续完成下列解题过程)
迁移拓展,深化运用:
如图6,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是$\sqrt{5}$-1.
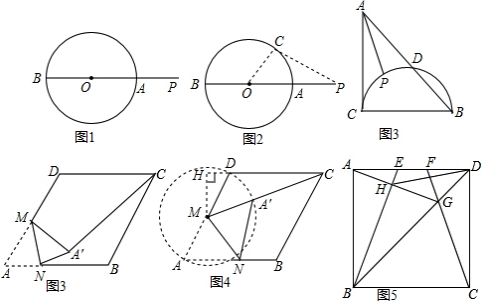
分析 探究:在⊙O上任取一点C(不为点A、B),连接PC、OC,证得PA<PC即可得到PA是点P到⊙O上的点的最短距离;
图中有圆,直接运用:找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,可见,AP1+EP1>AE,即AP2是AP的最小值,再根据勾股定理求出AE的长,然后减掉半径即可;
图中无圆,构造运用:根据题意得出A′的位置,进而利用锐角三角函数关系求出A′C的长即可;
迁移拓展,深化运用:根据正方形的性质可得AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,然后利用“边角边”证明△ABE和△DCF全等,根据全等三角形对应角相等可得∠1=∠2,利用“SAS”证明△ADG和△CDG全等,根据全等三角形对应角相等可得∠2=∠3,从而得到∠1=∠3,然后求出∠AHB=90°,取AB的中点O,连接OH、OD,根据直角三角形斜边上的中线等于斜边的一半可得OH=$\frac{1}{2}$AB=1,利用勾股定理列式求出OD,然后根据三角形的三边关系可知当O、D、H三点共线时,DH的长度最小.
解答 解:探究:
如图2,在⊙O上任取一点C(不为点A、B),连接PC、OC.
∵PO<PC+OC,PO=PA+OA,OA=OC,
∴PA<PC,
∴PA是点P到⊙O上的点的最短距离.(3分)
图中有圆,直接运用: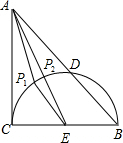 解:找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,
解:找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,
可见,AP1+EP1>AE,
即AP2是AP的最小值,
∵AE=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,P2E=1,
∴AP2=$\sqrt{5}$-1.
故答案为:$\sqrt{5}$-1;
图中无圆,构造运用:如图所示:∵MA′是定值,A′C长度取最小值时,即A′在MC上时,
过点M作MF⊥DC于点F,
∵在边长为2的菱形ABCD中,∠A=60°,M为AD中点,
∴2MD=AD=CD=2,∠FDM=60°,
∴∠FMD=30°,
∴FD=$\frac{1}{2}$MD=$\frac{1}{2}$,
∴FM=DM×cos30°=$\frac{\sqrt{3}}{2}$,
∴MC=$\sqrt{F{M}^{2}+C{F}^{2}}$=$\sqrt{7}$,
∴A′C=MC-MA′=$\sqrt{7}$-1.
故答案为:$\sqrt{7}$-1.
迁移拓展,深化运用:解:在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,
在△ABE和△DCF中,
$\left\{\begin{array}{l}{AB=CD}\\{∠BAD=∠CDA}\\{AE=DF}\end{array}\right.$,
∴△ABE≌△DCF(SAS),
∴∠1=∠2,
在△ADG和△CDG中,
$\left\{\begin{array}{l}{AD=CD}\\{∠ADG=∠CDG}\\{DG=DG}\end{array}\right.$,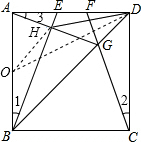
∴△ADG≌△CDG(SAS),
∴∠2=∠3,
∴∠1=∠3,
∵∠BAH+∠3=∠BAD=90°,
∴∠1+∠BAH=90°,
∴∠AHB=180°-90°=90°,
取AB的中点O,连接OH、OD,
则OH=AO=$\frac{1}{2}$AB=1,
在Rt△AOD中,OD=$\sqrt{A{O}^{2}+A{D}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
根据三角形的三边关系,OH+DH>OD,
∴当O、D、H三点共线时,DH的长度最小,
最小值=OD-OH=$\sqrt{5}$-1.
点评 本题考查了正方形的性质,全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,三角形的三边关系及圆的性质,确定出DH最小时点H的位置是解题关键,也是本题的难点.

 阅读快车系列答案
阅读快车系列答案
(1)完成下表的填空
| 正三角形个数 | 1 | 2 | 3 | 4 | … | n |
| 火柴棒根数 | 3 | 5 | 7 | 9 | … | 2n+1 |
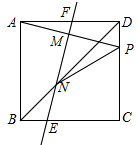 如图,正方形ABCD中,点P为CD上一点,线段AP的垂直平分线MN交BD于点N,点M为垂足,交两边于点E、F,连接PN,则下列结论,其中正确的有( )
如图,正方形ABCD中,点P为CD上一点,线段AP的垂直平分线MN交BD于点N,点M为垂足,交两边于点E、F,连接PN,则下列结论,其中正确的有( )①∠DNP=∠DAP;
②PC=$\sqrt{2}$BN;
③$\frac{DP+DC}{DN}$为常数;
④MN=MF+NE.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| x | … | -3 | -2 | -1 | 1 | 2 | 3 | … |
| y=-x+1 | … | 4 | 3 | 2 | 0 | -1 | -2 | … |
| y=-$\frac{2}{x}$ | … | $\frac{2}{3}$ | 1 | 2 | -2 | -1 | -$\frac{2}{3}$ | … |
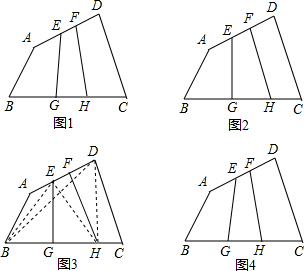 【提出问题】如图①,在四边形ABCD中,点E、F是AD的n等分点中最中间2个,点G、H是BC的n等分点中最中间2个,(其中n为奇数),连接EG、FH,那么S四边形EFHG与S四边形ABCD之间有什么关系呢?
【提出问题】如图①,在四边形ABCD中,点E、F是AD的n等分点中最中间2个,点G、H是BC的n等分点中最中间2个,(其中n为奇数),连接EG、FH,那么S四边形EFHG与S四边形ABCD之间有什么关系呢?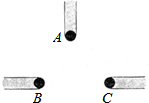 (1)如图是小刚(A)、小明(B)、小勇(C)和他们各自影子的俯视图,他们所构成三角形地形的内部有一盏路灯,你认为如图是在白天阳光下的俯视图还是在晚上这盏路灯下的俯视图?
(1)如图是小刚(A)、小明(B)、小勇(C)和他们各自影子的俯视图,他们所构成三角形地形的内部有一盏路灯,你认为如图是在白天阳光下的俯视图还是在晚上这盏路灯下的俯视图?