题目内容
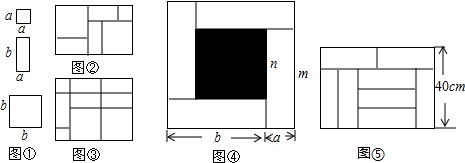
10.图a是一个长2m,宽2n的长方形,沿虚线平均分成四块,然后按图b拼成一个正方形.(1)图b中的阴影部分的面积表示为(m+n)2-4mn,并且有(m+n)2,(m-n)2,mn之间的等量关系为(m-n)2=(m+n)2-4mn;
(2)利用(1)的结论,思考:若x+y=-2,xy=-1.25,则x-y=±3;
(3)观察图c,利用图中表述的代数恒等式,思考:若方程2x2+3xy+y2=0(y≠0),则$\frac{x}{y}$=-1或-$\frac{1}{2}$;
(4)用图c中三个阴影图形,每个至少用一次,拼成一个面积为2m2+5mn+2n2长方形(图形之间不重叠无缝隙)画出图形(尽可能根原图一样标准并标出此长方形的长和宽)

分析 (1)阴影部分的面积=大正方形面积-4个长方形面积得出结论;
(2)代入(1)式计算即可;
(3)利用图b分解因式,解方程;
(4)仿照(3)画图,利用面积得出边长.
解答 解:(1)图b中的阴影部分的面积表示为:(m+n)2-4mn,还可以表示为:(m-n)2,
∴(m-n)2=(m+n)2-4mn,
故答案为:(m+n)2-4mn,(m-n)2=(m+n)2-4mn;
(2)(x-y)2=x2-2xy+y2,
=(x+y)2-4xy,
=(-2)2-4×(-1.25),
=9,
∴x-y=±3,
故答案为:±3;
(3)由图c得:(2m+n)(m+n)=2m2+3mn+n2,
2x2+3xy+y2=0,
(2x+y)(x+y)=0,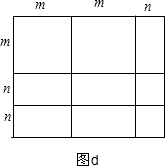
2x+y=0或x+y=0,
x=-$\frac{1}{2}$y或x=-y,
当x=-$\frac{1}{2}$y时,$\frac{x}{y}$=-$\frac{1}{2}$,
当x=-y时,$\frac{x}{y}$=-1,
故答案为:-1或-$\frac{1}{2}$;
(4)如图d,长方形面积为:(2m+n)(m+2n)=2m2+5mn+2n2.
点评 本题是完全平方公式的几何背景,运用几何直观理解、解决完全平方公式的推导过程,通过几何图形的面积对完全平方公式做出几何解释.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列图形表示y是x函数图象的个数是( )

| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
5.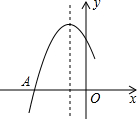 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,下列结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,下列结论:
①b2>4ac;
②2a+b=0;
③a+b+c>0;
④若B(-5,y1)、C(-1,y2 )为函数图象上的两点,则y1<y2.
其中正确结论是( )
 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,下列结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,下列结论:①b2>4ac;
②2a+b=0;
③a+b+c>0;
④若B(-5,y1)、C(-1,y2 )为函数图象上的两点,则y1<y2.
其中正确结论是( )
| A. | ②④ | B. | ①③④ | C. | ①④ | D. | ②③ |
14. 如图,等边△ABC的边长为3,F为BC边上的动点,FD⊥AB于D,FE⊥AC于E,则DE的长为( )
如图,等边△ABC的边长为3,F为BC边上的动点,FD⊥AB于D,FE⊥AC于E,则DE的长为( )
 如图,等边△ABC的边长为3,F为BC边上的动点,FD⊥AB于D,FE⊥AC于E,则DE的长为( )
如图,等边△ABC的边长为3,F为BC边上的动点,FD⊥AB于D,FE⊥AC于E,则DE的长为( )| A. | 随F点运动,其值不变 | B. | 随F点运动而变化,最大值为$\frac{9}{4}$ | ||
| C. | 随F点运动而变化,最小值为$\frac{9}{4}$ | D. | 随F点运动而变化,最小值为$\frac{3}{2}\sqrt{3}$ |
15.在△ABC中,AB=3,AC=2.当∠B最大时,BC的长是( )
| A. | 1 | B. | 5 | C. | $\sqrt{13}$ | D. | $\sqrt{5}$ |