题目内容
16. 如图,某足球运动员在离地面高度为h米的A处(点A在点O的正上方)凌空射门,足球的飞行高度y(单位:m)与飞行的水平距离x(单位:m)之间满足函数关系式y=-$\frac{1}{64}$x2+$\frac{1}{2}$x+k,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他若能将球直接射入球门,求k的取值范围.
如图,某足球运动员在离地面高度为h米的A处(点A在点O的正上方)凌空射门,足球的飞行高度y(单位:m)与飞行的水平距离x(单位:m)之间满足函数关系式y=-$\frac{1}{64}$x2+$\frac{1}{2}$x+k,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他若能将球直接射入球门,求k的取值范围.
分析 若要将球直接射入球门,则x=28时,0<y<2.44,列出关于k的不等式组,求解可得k的取值范围,结合点A在点O的正上方可得答案.
解答 解:根据题意知,当x=28时,0<y<2.44,
即$\left\{\begin{array}{l}{-\frac{1}{64}×2{8}^{2}+\frac{1}{2}×28+k>0}\\{-\frac{1}{64}×2{8}^{2}+\frac{1}{2}×28+k<2.44}\end{array}\right.$,
解得:-1.75<k<0.69,
又∵点A在点O的正上方,
∴k>0,
故0<k<0.69.
点评 本题主要考查二次函数的应用,根据题意理解将球直接射入球门时,即为x=28,0<y<2.44是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,依此类推,若OA1=1,则△A2016B2016A2017的边长为( )
如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,依此类推,若OA1=1,则△A2016B2016A2017的边长为( ) 如图,直角△ABC中,AB=5,BC=3,AC=4,直角△ABC将沿着它的一条边AB旋转一周,得到一个什么图形?试求出其表面积和点C运动的路程.
如图,直角△ABC中,AB=5,BC=3,AC=4,直角△ABC将沿着它的一条边AB旋转一周,得到一个什么图形?试求出其表面积和点C运动的路程.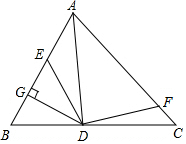 已知:如图所示,在△ABC中,AD是△ABC的角平分线,E、F分别是AB,AC上的点,并且有∠EDF+∠EAF=180°,DG⊥AB于点G.
已知:如图所示,在△ABC中,AD是△ABC的角平分线,E、F分别是AB,AC上的点,并且有∠EDF+∠EAF=180°,DG⊥AB于点G. 已知,如图,BC上有两点D、E,且BD=CE,AD=AE,∠1=∠2,求证:AB=AC.
已知,如图,BC上有两点D、E,且BD=CE,AD=AE,∠1=∠2,求证:AB=AC.