题目内容
△ABC中，∠A、∠B都是锐角，若sinA=
，cosB=
，则∠C= ．
| ||
| 2 |
| 1 |
| 2 |
考点：特殊角的三角函数值,三角形内角和定理
专题：计算题
分析：先根据特殊角的三角函数值求出∠A、∠B的度数，再根据三角形内角和定理求出∠C即可作出判断．
解答：解：∵△ABC中，∠A、∠B都是锐角sinA=
，cosB=
，
∴∠A=∠B=60°．
∴∠C=180°-∠A-∠B=180°-60°-60°=60°．
故答案为：60°．
| ||
| 2 |
| 1 |
| 2 |
∴∠A=∠B=60°．
∴∠C=180°-∠A-∠B=180°-60°-60°=60°．
故答案为：60°．
点评：本题考查的是特殊角的三角函数值及三角形内角和定理，比较简单．
练习册系列答案
相关题目
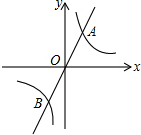如图，直线y=mx与双曲线y=
如图是由圆心角为30°，半径分别是1、3、5、7、…的扇形组成的图形，阴影部分的面积依次记为S1、S2、S3、…，则S14=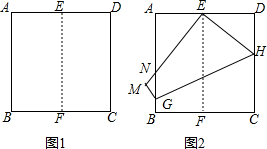
如图1，将正方形纸片ABCD对折，使AB与CD重合，折痕为EF．如图2，展开后再折叠一次，使点C与点E重合，折痕为GH，点B的对应点为点M，EM交AB于N，则tan∠ANE=
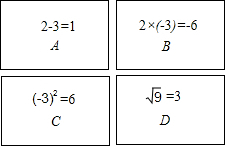如图，有四张卡片（形状、大小和质地都相同），正面分别写有字母A、B、C、D和一个不同的算式，将这四张卡片背面向上洗匀，从中随机抽取两张卡片，这两张卡片上的算式只有一个正确的概率是
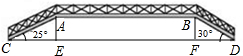如图是新城市建设中设计的一条人行过街天桥平面设计图，已知桥面AB与地面DC平行，立柱AE⊥CD于点E，立柱BF⊥CD于点F，CD=87.1m，CE=15m，∠ACE=25°，∠BDF=30°