题目内容
19. 如图,已知AB⊥AC于A,BD⊥DC于D,AC,BD相交于点E,AB=CD.证明:∠1=∠2.
如图,已知AB⊥AC于A,BD⊥DC于D,AC,BD相交于点E,AB=CD.证明:∠1=∠2.
分析 根据HL证明Rt△ABC与Rt△DCB全等,再利用全等三角形的性质证明即可.
解答 证明:∵AB⊥AC于A,BD⊥DC于D,
∴∠A=∠D=90°,
在Rt△ABC与Rt△DCB中
$\left\{\begin{array}{l}{AB=DC}\\{BC=CB}\end{array}\right.$,
∴Rt△ABC≌Rt△DCB(HL),
∴∠1=∠2
点评 此题考查全等三角形的判定和性质,关键是根据HL证明Rt△ABC与Rt△DCB全等.

练习册系列答案
相关题目
8. 如图所示,四边形ABCD中,AB=20,BC=15,CD=7,DA=24且∠B=90°,则四边形ABCD的面积为( )
如图所示,四边形ABCD中,AB=20,BC=15,CD=7,DA=24且∠B=90°,则四边形ABCD的面积为( )
 如图所示,四边形ABCD中,AB=20,BC=15,CD=7,DA=24且∠B=90°,则四边形ABCD的面积为( )
如图所示,四边形ABCD中,AB=20,BC=15,CD=7,DA=24且∠B=90°,则四边形ABCD的面积为( )| A. | 234 | B. | 235 | C. | 236 | D. | 237 |
9.函数y=(m+1)${x}^{{m}^{2}+1}$是二次函数,则m的值是( )
| A. | ±1 | B. | 1 | C. | -1 | D. | 以上都不对 |
 如图,∠ABC=90°,DE=BC,点E在AB上,∠ACD=45°,DE⊥BC于F
如图,∠ABC=90°,DE=BC,点E在AB上,∠ACD=45°,DE⊥BC于F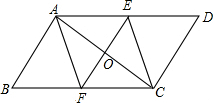 如图,已知在?ABCD中,点E、F分别在AD、BC上,O是AC的中点且EF⊥AC,求证:四边形AECF是菱形.
如图,已知在?ABCD中,点E、F分别在AD、BC上,O是AC的中点且EF⊥AC,求证:四边形AECF是菱形.