题目内容
已知x2+2x+1是多项式x3-x2+ax+b的因式,求a、b的值.
考点:因式分解的意义
专题:
分析:设x3-x2+ax+b=(x2+2x+1)(x+c),把等号右边的式子化简,合并同类项,与已知的式子对应项的系数相同,即可列方程求解.
解答:解:设x3-x2+ax+b=(x2+2x+1)(x+c),
则x3-x2+ax+b=(x2+2x+1)(x+c)
=x3+(c+2)x2+(2c+1)x+c,
则
,
解得:
.
即a=-5,b=-3.
则x3-x2+ax+b=(x2+2x+1)(x+c)
=x3+(c+2)x2+(2c+1)x+c,
则
|
解得:
|
即a=-5,b=-3.
点评:本题考查了因式分解的意义,以及代数式相等的条件,理解因式分解与整式的乘法互为逆运算是关键.

练习册系列答案
相关题目
已知代数式x3-2x2+ax+6,当x=-1时,它的值是0,则a的值是( )
| A、7 | B、3 | C、0 | D、-3 |

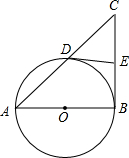 如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E是BC的中点.求证:DE是⊙O的切线.
如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E是BC的中点.求证:DE是⊙O的切线.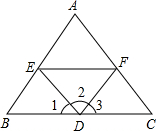 如图,请完成下列各题:
如图,请完成下列各题: 如图,在△ABC中,D是AB边上的点,以点D为顶点作∠ADE,使∠ADE=∠C,DE交边A C于点E.若AB=8,AC=6,AD=3,则AE=
如图,在△ABC中,D是AB边上的点,以点D为顶点作∠ADE,使∠ADE=∠C,DE交边A C于点E.若AB=8,AC=6,AD=3,则AE=