Question

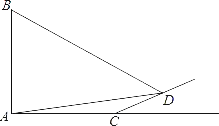
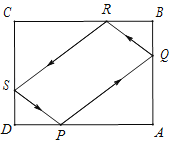
【题目】如图ABCD是一个矩形桌子，一小球从P撞击到Q，反射到R，又从R反射到S，从S反射回原处P，入射角与反射角相等（例如∠PQA＝∠RQB等），已知AB＝9，BC＝12，BR＝4．则小球所走的路径的长为_____．

Answer 1

【答案】30．

【解析】

证明四边形SPQR是平行四边形，推出SR＝PQ，PS＝QR，证三角形全等得出SR＝PQ，RQ＝PS，根据相似求出DS，根据勾股定理求出即RS，RQ，PQ，SP即可．

解：∵入射角与反射角相等，

∴∠BQR＝∠AQP，∠APQ＝∠SPD，∠CSR＝∠DSP，∠CRS＝∠BRQ，

∵四边形ABCD是矩形，

∴∠A＝∠B＝∠C＝∠D＝90°，

∴∠DPS+∠DSP＝90°，∠AQP+∠APQ＝90°，

∴∠DSP＝∠AQP＝∠CSR＝∠BQR，

∴∠RSP＝∠RQP，

同理∠SRQ＝∠SPQ，

∴四边形SPQR是平行四边形，

∴SR＝PQ，PS＝QR，

在△DSP和△BQR中

，

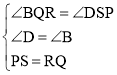∴△DSP≌△BQR（AAS），

∴BR＝DP＝4，BQ＝DS，

∵四边形ABCD是矩形，

AB＝CD＝9，BC＝AD＝112，

∴AQ＝9﹣DS，AP＝12﹣4＝8，

∵∠SPD＝∠APQ，

∴△SDP∽△QAP，

,

,

∴DS＝3，

在Rt△DSP中，由勾股定理得：PS＝QR＝，

同理PQ＝RS＝10，

∴QP+PS+SR+QR＝2×5+2×10＝30，

故答案为：30．