解方程组$\left\{\begin{array}{l}{5=2}\\{2=6}\end{array}\right.$若设=B.则原方程组可变形为$\left\{\begin{array}{l}{5A-3B=2}\\{2A+4B=6}\end{array}\right.$.解方程组得$\left\{\begin{array}{l}{A=1}\\{B=1}\end{array}\right.$.所以题目和参考答案——青夏教育精英家教网—

题目内容

16．解方程组$\left\{\begin{array}{l}{5（x+y）-3（x-y）=2}\\{2（x+y）+4（x-y）=6}\end{array}\right.$若设（x+y）=A，（x-y）=B，则原方程组可变形为$\left\{\begin{array}{l}{5A-3B=2}\\{2A+4B=6}\end{array}\right.$，解方程组得$\left\{\begin{array}{l}{A=1}\\{B=1}\end{array}\right.$，所以$\left\{\begin{array}{l}{x+y=1}\\{x-y=1}\end{array}\right.$解方程组得$\left\{\begin{array}{l}{x=1}\\{y=0}\end{array}\right.$，我们把某个式子看成一个整体，用一个字母去代替它，这种解方程组的方法叫换元法，请用这种方法解方程组$\left\{\begin{array}{l}{\frac{x+y}{2}+\frac{x-y}{3}=6}\\{2（x+y）-3x+3y=24}\end{array}\right.$．

分析设x+y=A，x-y=B，方程变形后，利用代入消元法求出A与B的值，进而确定出x与y的值即可．

解答解：设x+y=A，x-y=B，
方程组变形得：$\left\{\begin{array}{l}{\frac{A}{2}+\frac{B}{3}=6}\\{2A-3B=24}\end{array}\right.$，
整理得：$\left\{\begin{array}{l}{3A+2B=36①}\\{2A-3B=24②}\end{array}\right.$，
①×3+②×2得：13A=156，即A=12，
把A=12代入②得：B=0，
∴$\left\{\begin{array}{l}{x+y=12}\\{x-y=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=6}\\{y=6}\end{array}\right.$．

点评此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．

练习册系列答案

7．嗨，喜欢上网吗？现在互联网已经成为生活中不可缺少的一部分，假如您在“百度”搜索引擎中输入“乐陵”，能搜索到与之相关的网页约23300000个，将这个数用科学记数法表示为（　　）

4．中国拥有1.8万公里海岸线、300万平方公里的管辖海域，近海防御任务颇重．近年来，一些国家不时侵犯中国南海权益，令中国周边海域紧张局势加剧．若没有自己的航母，中国在东海与南海的正当权益难以有效保障，国内和平发展的大环境会受到侵蚀．中国航母辽宁舰是中国人民海军第一艘可以搭载固定翼飞机的航空母舰，满载排水量为67500吨，将67500吨用科学记数法表示为（　　）

11．从甲地到乙地有一段上坡与一段平路．如果保持上坡每小时走3千米，平路每小时走4千米，下坡每小时走5千米，那么从甲地到乙地需54分钟，从乙地到甲地需42分钟．根据以上条件，下列说法不正确的是（　　）

	A．	设上坡路长x千米，可列方程$\frac{x}{3}-\frac{x}{5}=\frac{54}{60}-\frac{42}{60}$
	B．	设上坡路长x千米，平路长y千米，可列方程组$\left\{\begin{array}{l}\frac{x}{3}+\frac{y}{4}=\frac{54}{60}\\ \frac{x}{5}+\frac{y}{4}=\frac{42}{60}.\end{array}\right.$
	C．	列算式（54-42）÷（5-3）即可求出上坡路长．
	D．	根据条件，能求出甲地到乙地的全程是3.1千米．

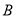已知中， .点从点出发沿线段移动，同时点从点出发沿线段的延长线移动，点、移动的速度相同，与直线相交于点.