题目内容
6. 如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3).
如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3).(1)请画出△ABC关于y轴对称的△DEF(其中D,E,F分别是A,B,C的对应点,不写画法);
(2)直接写出D,E,F三点的坐标:D(1,5),E(1,0),F(4,3);
(3)在y轴上存在一点,使PC-PB最大,则点P的坐标为(0,-1).
分析 (1)分别作出点A、B、C关于y轴对称点D、E、F,即可得△DEF;
(2)根据(1)中图形可得坐标;
(3)延长CB交y轴于P,点P即为所求,待定系数法求直线BC所在直线解析式,即可知其与y轴的交点P的坐标.
解答 解:(1)如图,△DEF即为所求作三角形;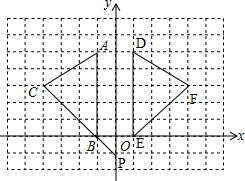
(2)由图可知点D(1,5)、E(1,0)、F(4,3),
故答案为:1,5;1,0;4,3;
(3)延长CB交y轴于P,此时PC-PB最大,故点P即为所求,
设BC所在直线解析式为y=kx+b,
将点B(-1,0)、点C(-4,3)代入,得:$\left\{\begin{array}{l}{-k+b=0}\\{-4k+b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=-1}\end{array}\right.$,
∴直线BC所在直线解析式为y=-x-1,
当x=0时,y=-1,
∴点P坐标为(0,-1),
故答案为:(0,-1).
点评 本题主要考查作图-轴对称变换及最短路线问题,作出三角形各顶点的对称点是作轴对称变换的关键,利用三角形三边关系是根据PC-PB最大确定点P位置的关键.

练习册系列答案
相关题目
4.中国拥有1.8万公里海岸线、300万平方公里的管辖海域,近海防御任务颇重.近年来,一些国家不时侵犯中国南海权益,令中国周边海域紧张局势加剧.若没有自己的航母,中国在东海与南海的正当权益难以有效保障,国内和平发展的大环境会受到侵蚀.中国航母辽宁舰是中国人民海军第一艘可以搭载固定翼飞机的航空母舰,满载排水量为67500吨,将67500吨用科学记数法表示为( )
| A. | 6.75×104吨 | B. | 67.5×103吨 | C. | 0.675×103吨 | D. | 6.75×10-4吨 |
14.如图,在平面直角坐标系中,用描点法分别画出函数y=-x+1与y=-$\frac{2}{x}$的图象,并写出不等式-x+1>-$\frac{2}{x}$的解集.
解:列表:
画图象:
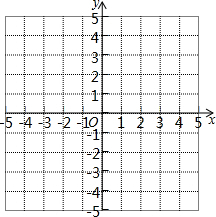
不等式-x+1>-$\frac{2}{x}$的解集为x<-1或0<x<2.
解:列表:
| x | … | … | ||||||
| y=-x+1 | … | … | ||||||
| y=-$\frac{2}{x}$ | … | … |

不等式-x+1>-$\frac{2}{x}$的解集为x<-1或0<x<2.
1. 如图,能判定EC∥AB的条件是( )
如图,能判定EC∥AB的条件是( )
 如图,能判定EC∥AB的条件是( )
如图,能判定EC∥AB的条件是( )| A. | ∠B=∠ACB | B. | ∠A=∠ACE | C. | ∠B=∠ACE | D. | ∠A=∠ECD |
11.化简$\sqrt{(m-5)^{2}(5-m)}$的正确结果是( )
| A. | (m-5)$\sqrt{5-m}$ | B. | (5-m)$\sqrt{5-m}$ | C. | m-5$\sqrt{-(5-m)}$ | D. | 5-m$\sqrt{5-m}$ |
18.在实数范围内,$\sqrt{x+1}$有意义,则x的取值范围是( )
| A. | x≥1 | B. | x≥-1 | C. | x≤1 | D. | x≤-1 |