题目内容
1.若(ax-4)(3x+n)计算结果为-6x2+mx-20,则a=-2,n=5,m=-22.分析 根据(ax-4)(3x+n)计算结果为-6x2+mx-20,可以将(ax-4)(3x+n)展开,然后找准和-6x2+mx-20对应的量,即可求得a、n、m的值,本题得以解决.
解答 解:∵(ax-4)(3x+n)计算结果为-6x2+mx-20,
∴(ax-4)(3x+n)=-6x2+mx-20,
∴3ax2+(an-12)x-4n=-6x2+mx-20,
∴$\left\{\begin{array}{l}{3a=-6}\\{an-12=m}\\{-4n=-20}\end{array}\right.$
解得,$\left\{\begin{array}{l}{a=-2}\\{n=5}\\{m=-22}\end{array}\right.$
故答案为:-2,5,-22.
点评 本题考查多项式乘以多项式,解题的关键是明确题意,找准对应关系.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
9.水果商贩小李去水果批发市场采购被誉为“果中之王”的泰顺猕猴桃,他了解到猕猴桃有精品盒与普通盒两种包装,精品盒的批发价格每盒60元,普通盒的批发价格每盒40元,现小李购得精品盒与普通盒共60盒,费用共为3100元.
(1)问小李分别购买精品盒与普通盒多少盒?
(2)小李经营着甲、乙两家店铺,每家店铺每天部能售出精品盒与普通盒共30盒,并且每售出一盒精品盒与普通盒,在甲店获利分别为30元和40元,在乙店获利分别为24元和35元.现在小李要将购进的60盒弥猴桃分配给每个店铺各30盒,设分配给甲店精品盒a盒,请你根据题意填写下表:
小李希望在甲店获利不少于1000元的前提下,使自己获取的总利润W最大,应该如何分配?最大的总利润是多少?
(1)问小李分别购买精品盒与普通盒多少盒?
(2)小李经营着甲、乙两家店铺,每家店铺每天部能售出精品盒与普通盒共30盒,并且每售出一盒精品盒与普通盒,在甲店获利分别为30元和40元,在乙店获利分别为24元和35元.现在小李要将购进的60盒弥猴桃分配给每个店铺各30盒,设分配给甲店精品盒a盒,请你根据题意填写下表:
| 精品盒数量(盒) | 普通盒数量(盒) | 合计(盒) | |
| 甲店 | a | 30-a | 30 |
| 乙店 | 35-a | a-5 | 30 |
13.已知$\sqrt{{(1-2x)}^2}=2x-1$,则x的取值范围是( )
| A. | x≥$\frac{1}{2}$ | B. | x≤$\frac{1}{2}$ | C. | x>$\frac{1}{2}$ | D. | x<$\frac{1}{2}$ |
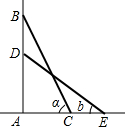 如图,一架梯子斜靠在墙上,梯子与地面的夹角为a(a=∠BCA),当梯顶下滑1m时,这架梯子与地面的夹角为b(b=∠DEA,A、C、E三点在一条直线上),求梯子的长.
如图,一架梯子斜靠在墙上,梯子与地面的夹角为a(a=∠BCA),当梯顶下滑1m时,这架梯子与地面的夹角为b(b=∠DEA,A、C、E三点在一条直线上),求梯子的长.