题目内容
10. 如图,△OAB与△OCD都是等边三角形,连接AC、BD相交于点E.
如图,△OAB与△OCD都是等边三角形,连接AC、BD相交于点E.(1)求证:①△OAC≌△OBD,②∠AEB=60°;
(2)连结OE,OE是否平分∠AED?请说明理由.
分析 (1)①根据SAS即可判定.②由△OAC≌OBD,推出∠OAE=∠OBD,由△OAB是等边三角形,推出∠OAB+∠OBA=120°,推出∠OAE+∠BAE+∠OBA=120°,即∠EAB+∠EBA=120°,推出∠AEB=60°.
(2)OE平分∠AED.作OM⊥AC于M,ON⊥BD于N.由△OAC≌△OBD,推出S△OAC=S△OBD,推出$\frac{1}{2}$•AC•OM=$\frac{1}{2}$•BD•ON,推出OM=ON,再根据角平分线判定定理即可证明.
解答 (1)证明:①∵△OAB与△OCD都是等边三角形,
∴OA=OB,OC=OD,∠AOB=∠COD=60°,
∴∠AOB+∠BOC=∠COD+∠BOC,
即∠AOC=∠BOD,
∴△OAC≌△OBD.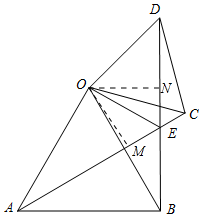
②∵△OAC≌OBD,
∴∠OAE=∠OBD,
∵△OAB是等边三角形,
∴∠OAB+∠OBA=120°,
∴∠OAE+∠BAE+∠OBA=120°,
即∠EAB+∠EBA=120°,
∴∠AEB=60°.
(2)解:OE平分∠AED.理由如下:
作OM⊥AC于M,ON⊥BD于N.
∵△OAC≌△OBD,
∴S△OAC=S△OBD,
∴$\frac{1}{2}$•AC•OM=$\frac{1}{2}$•BD•ON,
∴OM=ON,
∴OE平分∠AED.
点评 本题考查全等三角形的判定和性质、角平分线的判定等知识,解题的关键是灵活运用全等三角形的性质解决问题,学会利用面积法证明线段相等,属于中考常考题型.

练习册系列答案
相关题目
15.一元二次方程x2-2x-5=0根的判别式的值是( )
| A. | 24 | B. | 16 | C. | -16 | D. | -24 |
2.如果一个多边形中,经过每一个顶点都有6条对角线,那么这个多边形是( )
| A. | 七边形 | B. | 八边形 | C. | 九边形 | D. | 十边形 |
19.下列多项式相乘,结果为x2-4x-12的是( )
| A. | (x-4)(x+3) | B. | (x-6)(x+2) | C. | (x-4)(x-3) | D. | (x+6)(x-2) |
20.在平面直角坐标系中,若点A(a,b)在第四象限内,则点B(a,-b)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 已知正方形ABCD,M、N两动点分别从A、C两点同时出发沿正方形的边开始移动,点M按逆时针方向移动,点N按顺时针方向移动,若点M的速度是点N的4倍,则它们第2017次相遇在边AB上.
已知正方形ABCD,M、N两动点分别从A、C两点同时出发沿正方形的边开始移动,点M按逆时针方向移动,点N按顺时针方向移动,若点M的速度是点N的4倍,则它们第2017次相遇在边AB上.
 如图AD∥BC,∠A=30°,∠D=70°,作射线CE∥AB,则∠DCE=80°或100°.
如图AD∥BC,∠A=30°,∠D=70°,作射线CE∥AB,则∠DCE=80°或100°.