题目内容
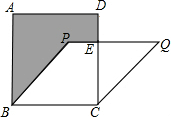 如图所示,正方形ABCD与菱形PQCD的面积分别为25cm2和20cm2,阴影部分的面积为
如图所示,正方形ABCD与菱形PQCD的面积分别为25cm2和20cm2,阴影部分的面积为考点:菱形的性质,正方形的性质
专题:
分析:由题意易得AB=BC=BP=PQ=QC=5,EC=4,在Rt△QEC中,可根据勾股定理求得EQ=3,又有PE=PQ-EQ=2,进而可得S阴影的值.
解答:解:∵正方形ABCD的面积是25cm2,
∴AB=BC=BP=PQ=QC=5cm,
又∵S菱形BPQC=PQ×EC=5×EC=20cm2,
∴S菱形BPQC=BC•EC,
即20=5•EC,
∴EC=4cm2,
在Rt△QEC中,EQ=
=3cm;
∴PE=PQ-EQ=2cm,
∴S阴影=S正方形ABCD-S梯形PBCE=25-
×(5+2)×4=25-14=11(cm2)
故答案为:11.
∴AB=BC=BP=PQ=QC=5cm,
又∵S菱形BPQC=PQ×EC=5×EC=20cm2,
∴S菱形BPQC=BC•EC,
即20=5•EC,
∴EC=4cm2,
在Rt△QEC中,EQ=
| QC2-EC2 |
∴PE=PQ-EQ=2cm,
∴S阴影=S正方形ABCD-S梯形PBCE=25-
| 1 |
| 2 |
故答案为:11.
点评:本题考查了菱形的性质和面积,正方形的性质的应用,能综合运用性质进行计算是解此题的关键,难度适中.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
菱形的周长为100cm,一条对角线长为14cm,它的面积是( )
| A、168cm2 |
| B、336cm2 |
| C、672cm2 |
| D、84cm2 |
 请制作如图所示的纸帽,使纸帽的高为30cm,底面半径为16cm(要求画出纸帽的侧面展开图的示意图,并标明尺寸).
请制作如图所示的纸帽,使纸帽的高为30cm,底面半径为16cm(要求画出纸帽的侧面展开图的示意图,并标明尺寸).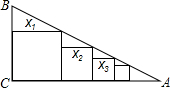 如图,在Rt△ABC中,∠C=90°,BC=a,AC=b,在△ABC中依次放入边长为x1,x2,x3,…,xn的正方形,试用a、b表示这些正方形的边长.
如图,在Rt△ABC中,∠C=90°,BC=a,AC=b,在△ABC中依次放入边长为x1,x2,x3,…,xn的正方形,试用a、b表示这些正方形的边长.
 一个正方形ABCD的相邻边分别为x轴,y轴平行,且面积为9,A(1,2),试结合图形求顶点C的坐标.
一个正方形ABCD的相邻边分别为x轴,y轴平行,且面积为9,A(1,2),试结合图形求顶点C的坐标. 在平面直角坐标系xOy中,抛物线y=x2-(m+n)x+mn(m>n)与x轴相交于A、B两点(点A位于点B的右侧),与y轴相交于点C,若m=2,n=1,求A、B两点的坐标.
在平面直角坐标系xOy中,抛物线y=x2-(m+n)x+mn(m>n)与x轴相交于A、B两点(点A位于点B的右侧),与y轴相交于点C,若m=2,n=1,求A、B两点的坐标.