题目内容
17.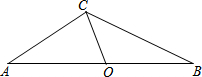 如图,已知钝角三角形ABC,∠A=35°,OC为边AB上的中线,将△AOC绕着点O顺时针旋转,点C落在BC边上的点C′处,点A落在点A′处,联结BA′,如果点A、C、A′在同一直线上,那么∠BA′C′的度数为20°.
如图,已知钝角三角形ABC,∠A=35°,OC为边AB上的中线,将△AOC绕着点O顺时针旋转,点C落在BC边上的点C′处,点A落在点A′处,联结BA′,如果点A、C、A′在同一直线上,那么∠BA′C′的度数为20°.
分析 根据旋转的性质得出OA=OA′,∠OA′C′=∠A=35°,根据三角形外角的性质从而求得∠AOB=70°,证得OA′=OB,根据等边对等角,得出∠OA′B=∠OBA′=55°,进而就可求得∠BA′C′=55°-35°=20°.
解答 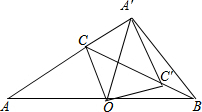 解:如图,将△AOC绕着点O顺时针旋转,点C落在BC边上的点C′处,点A落在点A′处,
解:如图,将△AOC绕着点O顺时针旋转,点C落在BC边上的点C′处,点A落在点A′处,
则OA=OA′,∠OA′C′=∠A=35°
∴∠OA′A=∠A=35°,
∴∠A'OB=70°
∵OC为边AB上的中线,
∴OA=OB,
∴OA′=OB,
∴∠OA′B=∠OBA′=55°,
∴∠BA′C′=55°-35°=20°.
故答案为20°.
点评 本题考查了旋转的性质,等腰三角形的判定和性质,三角形外角的性质,三角形的内角和定理,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
8.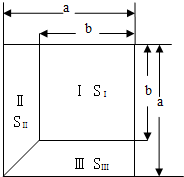 根据图示,回答下列问题
根据图示,回答下列问题
(1)大正方形的面积S是多少?
(2)梯形Ⅱ,Ⅲ的面积SⅡ,SⅢ,分别是多少?
(3)试求SⅡ+SⅢ与S-SⅠ的值.
(4)由 (3)你发现了什么?请用含a,b的式子表示你的结论.
 根据图示,回答下列问题
根据图示,回答下列问题(1)大正方形的面积S是多少?
(2)梯形Ⅱ,Ⅲ的面积SⅡ,SⅢ,分别是多少?
(3)试求SⅡ+SⅢ与S-SⅠ的值.
(4)由 (3)你发现了什么?请用含a,b的式子表示你的结论.
5.6名学生中,初一、初二、初三各占2名,若从这6名学生中任意选取3名,实验估计选取的3名学生中,两两不在同一年段的概率,那么下列实物可以直接作为模拟实验中的替代物的是( )
| A. | 6个只有颜色不同的小球 | |
| B. | 两个骰子 | |
| C. | 三个硬币 | |
| D. | 只有颜色不同的小卡片6张,其中红、白、黄各占2张 |
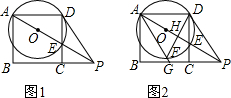 如图1,已知ABCD是边长为4的正方形,E是CD边上的一个动点,连接AE,AE的延长线交BC的延长线于点P,连接PD.作△ADE的外接圆⊙O.设DE=x,PC=y.
如图1,已知ABCD是边长为4的正方形,E是CD边上的一个动点,连接AE,AE的延长线交BC的延长线于点P,连接PD.作△ADE的外接圆⊙O.设DE=x,PC=y. 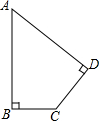 如图,已知一块四边形草地ABCD,其中∠A=45°,∠B=∠D=90°,AB=20m,CD=10m,求这块草地的面积.
如图,已知一块四边形草地ABCD,其中∠A=45°,∠B=∠D=90°,AB=20m,CD=10m,求这块草地的面积.